El programa Bichos puede descargarse en este enlace. Es un archivo ejecutable (Bichos_2024_FC.exe) que no requiere instalación y debería iniciarse simplemente haciendo doble clic sobre él. Por tratarse de un ejecutable, es posible que el navegador o Windows lo consideren sospechoso de contener un virus, lo cual no es el caso. Si al intentar iniciarlo aparece un mensaje de Windows diciendo que es potencialmente peligroso, debajo del mensaje debería haber una opción, "Más información", que permite ejecutarlo de todos modos. Si el navegador, Windows o el propio usario persisten en su natural desconfianza, pueden escribirme a arieldr74@gmail.com.
El programa lo he probado en Windows 10, con todas las librerías de VB instaladas, y también en Windows 11, sin ningún otro programa instalado.

Ventana de inicio

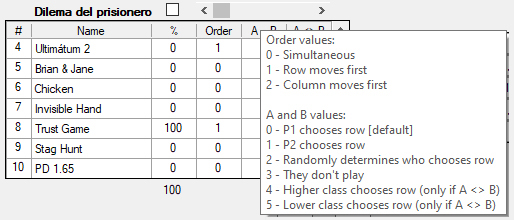
La ventana de inicio del programa muestra un juego para dos jugadores en forma normal. Se puede seleccionar uno de los diez juegos disponibles en la lista de juegos [1], entre los que están el dilema del prisionero, el gallina y el ultimátum, entre otros. Para seleccionar uno, basta con hacer clic en el nombre correspondiente. El usuario puede también editar la matriz designada como Matrix 0 [2] para introducir pagos que definan cualquier otro juego. Para ello, debe hacer clic en la casilla cuyo valor quiera cambiar. La forma más sencilla para moverse rápidamente dentro de la matriz de pagos es pulsando la tecla Tab.

            Como es habitual, cada resultado del juego consta de dos pagos: el de la izquierda es el del jugador que elige filas (jugador filas = jF) y el de la derecha, el del jugador que elige columnas (jugador columnas = jC). En la figura 1, Matrix 0, tenemos un dilema del prisionero en el que pueden elegirse grados de mayor o menor cooperación, y no sólo los extremos habituales de cooperar y defraudar. Así, cada jugador puede elegir entre cinco estrategias diferentes. Por ejemplo, la esquina superior izquierda representa el resultado de la cooperación mutua. Los resultados se representan como la intersección del par de elecciones tomadas por los jugadores, según el número de fila o columna, separados por un punto y coma. Las filas se numeran de arriba abajo y las columnas de izquierda a derecha. Además, si procede indicar el pago que un cierto resultado ofrece a cada jugador, se indica la cifra a continuación de la fila o columna escogida, separada por el signo de igualdad. Por tanto, el resultado de la esquina superior izquierda y los pagos que obtienen jF y jC se expresan como F1 = 3 ; C1 = 3.

            Se pueden cambiar las dimensiones del juego con las flechas verticales y horizontales [3] para definir así juegos en el rango que va de 2 × 2 a 5 × 5. Para que el juego se presente luego en el mundo, hay que asignarlo a la lista de juegos [1] haciendo clic en el botón “Assign to” [4]; con la barra horizontal que hay debajo de ella se selecciona la posición que ocupará en la lista.

            Con estas variaciones se pueden definir juegos con pagos simétricos o asimétricos, de suma cero o no cero. Más adelante veremos que pueden ser también de información completa o incompleta, con decisiones simultáneas o sucesivas.

[001]

            La matriz de pagos Matrix 0 [2] representa el juego objetivo o real. Esto significa que los pagos corresponden a estados de cosas reales: cantidad de dinero, años de prisión o, por poner un ejemplo poco habitual, la longitud de onda de un color. Llamaré pagos materiales a estas magnitudes que representan el rendimiento adaptativo (differential reproductive fitness) de un agente o individuo, es decir, la cantidad de descendientes que tiene en relación a la cantidad media de descendientes de todos los individuos de una población: “In a biological context, a payoff is understood to be ‘average incremental fitness’. That is to say, a player’s success in the game is measured in terms of how many extra children the player can expect to have on average as a consequence of the way the game is played.” (Binmore, Game Theory and the Social Contract: Vol. 1 Playing Fair, p. 98)

            Las matrices de pagos Matrix 1 [5] y Matrix 2 [6] representan cómo jF y jC, respectivamente,  “perciben” el juego. En cualquiera de las tres matrices, Matrix 0, 1 o 2, el par de casillas marcadas en verde y rojo representan el resultado del juego: en verde el pago que obtiene jF, y en rojo el que obtiene jC. En Matrix 1 y Matrix 2 los pagos que se muestran son ordinales y reducidos a una escala que va de 0 a 1, de ahí que sean diferentes de los mostrados en Matrix 0; más adelante explico en detalle la necesidad de esta transformación y cómo se lleva a cabo.

La expresión “percepción del juego” significa que los jugadores, al evaluar los pagos de Matrix 0 como objetos de sus preferencias, generan otros dos juegos, Matrix 1 [5] y Matrix 2 [6], donde los jugadores toman realmente sus decisiones. La conversion de Matrix 0 en Matrix 1 y Matrix 2 se produce al aplicar a los pagos de Matrix 0 determinadas funciones de utilidad que reflejan el orden de preferecias de los jugadores sobre los resultados de Matrix 0. La función de utilidad incorpora como argumentos tanto los pagos materiales propios como los del otro jugador, tal como aparecen en Matrix 0.

            Por ejemplo, la función de utilidad de jF podría ser u_f = p_f + p_c, donde p_f y p_c son los respectivos pagos materiales de jF y jC en Matrix 0. Por ejemplo, una función de utilidad totalmente egoísta sería u_f = p_f, una completamente altruista sería u_f = p_c y la función de utilidad utilitarista sería u_f = p_f + p_c, etc.

            Así, las funciones de utilidad pueden expresar las llamadas “preferencias vicarias” (others-regarding preferences). Supongamos que la función de utilidad u_f = p_f representa las preferencias de jF en situaciones donde solo sus propios pagos están en juego. Debe decidir, por ejemplo, si saldrá o no con un paraguas en previsión de que pueda llover, y las consecuencias de la decisión sólo le afectan a él. Pero "adopta" otra función u_f = p_f + p_c cuando sus decisions afectan a terceros. Cómo sean posibles estos cambios y la metáfora de que un agente “tenga” una función de utilidad que lo determina a actuar, son recursos de un modelo para dar cuenta de un hecho empírico, a saber, que las preferencias sobre un mismo conjunto de objetos varían según cómo dichos conjuntos se relacionan con diversos agentes: 5 manzanas son siempre más que 3 manzanas, pero puedo preferir 5 a 3 si estoy solo o 3 a 5 si hay otra persona interesada en las manzanas.

            En la teoría de la utilidad se asignan funciones de utilidad a los agentes con el fin de explicar sus comportamientos, es decir, como si sus preferencias fueran las reflejadas en la función de utilidad. Pero los agentes artificiales del modelo tienen realmente funciones de utilidad en el sentido de que éstas son parte de las causas que determinan sus decisiones.

            Cada jugador tiene dos conjuntos de funciones de utilidad. En el primer conjunto, U, se encuentran funciones como las que acabamos de ver, empleadas para evaluar los pagos materiales, determinando así las preferencias sobre los resultados del juego material. El segundo conjunto de funciones, V, es similar al primero, pero sus funciones son las que un jugador (por ejemplo jF) supone que son las funciones de utilidad del otro jugador (jC). Con una función de U y otra de V, cada jugador genera los pagos que configuran un juego “subjetivo”, que es el juego en el que realmente se toman las decisiones. Estos juegos subjetivos se representan en Matrix 1 para jF y en Matrix 2 para jC. Una función v es en último término una forma de adivinar cuáles son las preferencias del otro jugador y, en este sentido, no son el modelo más elemental en teoría de juegos, sino que constituyen un refinamiento que contempla los llamados juegos de información incompleta.

            Consideremos este DP:

[002]

 

Las casillas en colores indican cuál ha sido el resultado del juego, que no coincide con el punto de equilibrio (F2 ; C2). En efecto, jF ha elegido la fila 2 (elección racional), pero jC ha sido irracional y ha elegido la columna 1. Para darle sentido a este resultado que viola las condiciones de la teoría, tenemos que analizar cómo ven jF y jC el juego material a través de sus funciones de utilidad. jF está jugando al siguiente juego, que replica los pagos materiales y en el cual, según sus expectativas, jC elegirá C2, tal como prescribe la teoría:

[003]

 

La función u_f es completamente egoísta (Ego = 1), como también lo es v_f, la función que jF atribuye a jC. Sin embargo, jC está jugando a otro juego, configurado por las dos funciones de utilidad de jC, u_c y v_c, que son completamente altruistas (Alter = 1):

 

[004]

           

     En Matrix 2 podemos observar que la estrategia dominante de jC no es C2, sino C1.

         En definitiva, jF es un egoísta que piensa que jC es otro egoísta, y jC es un altruista que ve en jF a otro altruista (ambos ladrones creen que todos son de su condición). Ahora bien, una vez definidos los juegos a los que cada uno está realmente jugando (Matrix 1 y Matrix 2), ambos son maximizadores racionales.

            Como ninguno de los dos conoce realmente las preferencias del otro, sino que deben emplear una función v a modo de conjetura, estamos ante un juego de información incompleta. Para tener el modelo más básico que propone la teoría de juegos, y que las preferencias de ambos jugadores sean de conocimiento común, podemos marcar la casilla Complete information (véase supra [7] en la figura 1).

            Al marcar esta casilla, v_f adquiere la auténtica función de utilidad u_c y, del mismo modo, v_c adquiere el valor de u_f (ni v_f ni v_c pueden modificarse mientras Complete information esté marcada). Ahora sí, ambos jugadores conocen las preferencias del otro y están jugando ambos al mismo juego: Matrix 1 y Matrix 2 coinciden exactamente en todos los resultados.

[005]

 

            Sin embargo, conviene insistir en que incluso si las matrices de pagos “subjetivas” de jF y jC son idénticas, no tienen por qué coincidir (de hecho, raramente lo harán), con la matriz de pagos material Matrix 0).

            En los juegos secuenciales, es decir, cuando un jugador (jF, por ejemplo) elige primero y el otro (jC) toma su decisión a continuación, ocurre necesariamente que jC conoce con seguridad las preferencias (reveladas en la acción) de jF, mientras que jF sólo puede aventurar mediante v_f cuáles son las preferencias de jC.

            Veamos ahora con más detalle cómo se forman en la simulación las funciones de utilidad. En lo que sigue, describiré una serie de variables desde el punto de vista de jF. Así, el egoísmo de jF consiste en tener en consideración sólo los pagos de jF, pero para jC consistiría en atender sólo a los pagos de jC.

          Una función de utilidad toma como argumentos los pagos materiales de jF y jC en cada resultado del juego, tal como aparecen en Matrix 0, y les asigna ciertos pesos relativos, es decir, una mayor o menor importancia expresada mediante tres magnitudes que operan sobre los argumentos. Estas magnitudes son el egoísmo (sobre los pagos de jF), el altruismo (sobre los pagos de jC) y la equidad (sobre la diferencia entre los pagos de jF y los de jC). En la simulación aparecen como “Ego”, “Alter” y “Equity”, pero aquí las designaré como α, β y γ, tales que α + β + γ= 1

            El valor de la función es la utilidad que un determinado resultado del juego material, considerando tanto los pagos de jF como los de jC, tiene para jF. Esta utilidad conforma los pagos del juego subjetivo, que es donde el agente toma realmente su decisión. Así, por ejemplo, en Matrix 1 y Matrix 2, y atendiendo al resultado correspondiente a las decisiones F3 ; C3, tenemos:

[006]

 

 

a) La utilidad (0.9) que el resultado le reporta a jF, según la función de utilidad u_f.

b) La utilidad (0.55) que el resultado le reporta a jC, según la que jF estima que es la función de utilidad de jC, v_f.

c) La utilidad (0.57) que el resultado le reporta a jC, según la función de utilidad u_c.

d) La utilidad (0.92) que el resultado le reporta a jF, según la que jC estima que es la función de utilidad de jF, v_c.

            A cada función de utilidad le corresponde un número único (ID), generado por cada combinación de los valores que pueden tener las variables Ego (α), Alter (β) y Equity (γ). Por ejemplo, la función de utilidad más egoísta, que deposita el 100 % de su valor en Ego, tiene el número 231 (es la función por defecto en la pantalla de inicio del programa).

            Recapitulando, una función de utlidad, u, consta de seis parámetros. Tres de ellos (p_f, p_c y z) están tomados de los pagos materiales del juego original: p_f y p_c son los pagos materiales de jF y jC para un cierto resultado, mientras que z refleja el grado de equidad entre p_f y p_c, según una serie de operaciones que veremos a continuación. Los otros tres parámetros (α, β, γ) representan la importancia relativa que el jugador asigna a p_f, p_c y z. Así, pues, las funciones de utilidad tienen la forma general u = (p_p, p_a), donde p_p significa "pago propio" y p_a significa "pago ajeno" (cualquiera de los dos puede ser p_f o p_c, según el punto de vista que consideremos)

u = p_p α + p_a β + z γ

Como habíamos indicado más arriba, se debe cumplir que

α + β + γ= 1

Por su parte, z es una relación entre p_p y p_a, que tiene la siguiente forma:

z = ( |max – min| – |p_p – p_a| )

Max y min son el mayor y el menor pago posible, respectivamente, que cualquiera de los dos jugadores puede obtener en el juego. El propósito es que z sea un índice de equidad de cada resultado del juego, relacionando la diferencia entre un cierto par de pagos de un resultado real, |p_p – p_a|, y la máxima diferencia posible entre los pagos máximo y mínimo de cualquier jugador, |max – min|. Quizá sería más correcto expresarlo como una relación:

o bien

pero estas formulaciones tienen el inconveniente de que el denominador podría ser 0.

Una vez calculados los pagos subjetivos de cada jugador, según la fórmula

u = p_p α + p_a β + z γ

que también puede expresarse descomponiendo z:

u = p_p α + p_a β + ( |max – min| – |p_p – p_a| ) γ

se convierten todos ellos a una escala que va de 0 a 1.

Así, γ = 1 representa la función de utilidad que generará los pagos más equitativos posibles, mientras que γ = 0, los menos equitativos, dadas las circunstancias dadas por la naturaleza del juego. Con esto quiero decir, por ejemplo, que en este juego:

[007]

el resultado del juego objetivo F1 = 4 ; C1 = 5 no es perfectamente equitativo, pero sí es el más equitativo de los cuatro resultados posibles, sobre todo teniendo en cuenta la diferencia entre el menor y el mayor pago, 0 y 8, que el juego ofrece a cualquiera de los dos jugadores. Así, los resultados, de más a menos equitativos, son:

                                                           1.°       γ = ( |8 – 0| – |4 – 5| ) = 7

                                                           2.°       γ = ( |8 – 0| – |0 – 2| ) = 6

                                                           3.°       γ = ( |8 – 0| – |3 – 0| ) = 5

                                                           4.°       γ = ( |8 – 0| – |1 – 8| ) = 1

Puesto que se concede toda la importancia a la equidad, γ = 1, los valores de z se conservan tal como aparecen en esta clasificación ordinal. Y si ahora reducimos dicha clasificación a una escala que va de 1 (primer puesto) a 0 (último puesto), la utilidad ordinal de los cuatro resultados posibles será: 1, 0.67, 0.33 y 0, tal como se ve en la figura 7.

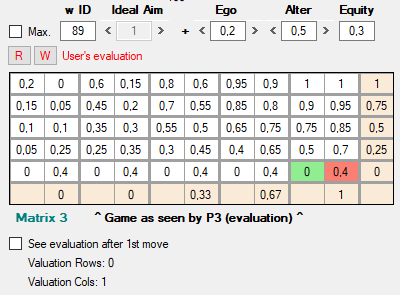
Además de los conjuntos U y V, cada agente cuenta con una función de utilidad adicional, w, que opera también sobre los pagos materiales (Matrix 0), y cuyo resultado se muestra en Matrix 3 [8], debajo de la lista de juegos. A diferencia de u y v, la función w sirve para evaluar las decisiones que de hecho ya se han producido en el juego, una vez que ambos jugadores las han tomado. Algunas consideraciones al respecto:

1) La función w puede ser cualquiera de las 462 (231 positivas y 231 negativas) que pueden encontrarse en U y V, pero se la considera separadamente para permitir una mayor flexibilidad en el modo en que los agentes evalúan conductas y reaccionan a ellas. (Las funciones negativas se explican más adelante).

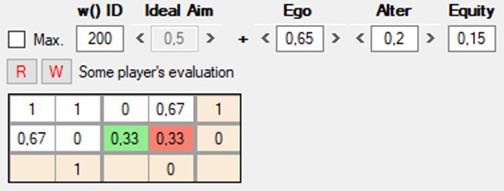
2) Ahora sólo estamos viendo la ventana inicial del programa. Más adelante, cuando pasemos el mundo virtual y examinemos cualquiera de las decisiones tomadas por sus habitantes, en Matrix 3 se mostrará la w que un determinado jugador ha empleado para evaluar un resultado. En cualquier momento, ya sea en esta pantalla inicial o durante la evolución del mundo, el usuario puede introducir en Matrix 3 una función w arbitraria (en el ejemplo de abajo, la número 105). Esto permitirá evaluar las decisiones de los jugadores virtuales desde un punto de vista que el usuario considere razonable con el fin de medir, por ejemplo, el grado de cooperación que esté alcanzando la población.

3) Las w de los jugadores están originalmente determinadas al azar y pueden ser totalmente ajenas a nuestras intuiciones de lo que sean la racionalidad o la moralidad. Es importante no confundir la w del usuario con las de los agentes artificiales. La w del usuario queda señalada en rojo (User’s evaluation) y tiene dos botones, W para escribir y R para leer:

[008]

Con W (write) podemos guardar la w que definamos como nuestro punto de vista, y con R (read) podemos recuperarla para sustituir cualquier otra que se estuviese mostrando. Cuando la w mostrada es la de algún jugador del mundo virtual, se indica en negro como Some player’s evaluation.

[2024_06_05_B.jpg]

          En 008 vemos que en esta ocasión w es la función 105 (Ego = 0.25, Alter = 0.45, Equity = 0.3). Se trata de una función que refleja ciertas intuiciones morales comunes para nosotros. Por ejemplo, genera el mayor de todos los pagos (1) para el resultado de la mutua cooperación en el DP (esquina superior izquierda [1]). Con w = 105 seleccionada, si vamos pasando por otros juegos de la lista, veremos que sigue asignando 1 a los resultados que nos parecerían más decentes y razonables. Dado que w = 105 y otras w similares pueden estar en el repertorio de funciones de los jugadores virtuales, estos pueden comportarse como agentes “universales”, capaces de evaluar cualquier situación o juego sin tener que indicarles por adelantado qué columna o qué fila representan el vicio o la virtud. [No estoy al corriente de todas las simulaciones existentes, y menos aún las más recientes, pero esta característica no la he visto aún en otros programas].

4) Es importante notar que en Matrix 3 se evalúan simultáneamente las decisiones y resultados de ambos jugadores (el de las filas y el de las columnas). Al aplicar w, un jugador está evaluando tanto los resultados y la acción del otro jugador como los suyos propios.

Por ejemplo, consideremos los pagos materiales (Matrix 0) y una interacción en la que jF ha elegido la columna superior (F1) y jC ha elegido la columna derecha (C2).

[010]

Los pagos materiales de este resultado son F1 = 0.5 ; C2 = 4. Es decir, jC ha obtenido mucho más que jF, pero si miramos Matrix 3 vemos que w  = 105 valora con 0.67 (bastante positivo) a jF y con 0, la peor evaluación posible, a jC. El juego considerado en Matrix 0 es un DP, y una racionalización elemental de este juicio sería la desaprobación de que jC haya explotado a jF y que, si bien nos parece loable la cooperación de jF, podemos censurarle cierta ingenuidad por su cooperación no correspondida; después de todo, w = 105 concede algo de importancia a los intereses propios (Ego = 0.25).

4.1) De manera intencionada, el juego representado en Matrix 0 es un DP ligeramente asimétrico, ya que tenemos por un lado F1 = 0.5 ; C2 = 4 y, por otro, F2 = 4 ; C1 = 0. Pero es un DP de todos modos y w = 105 lo reconoce adecuadamente como tal.

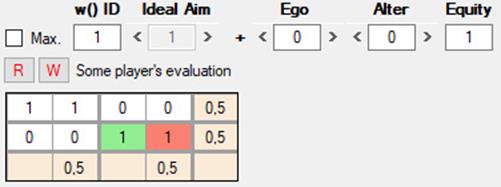
            Con la misma Matrix 0 del DP, pero ahora con w = 1, a la que sólo le importa la equidad (Ego = 0, Alter = 0, Equality = 1), vemos que produce el mismo pago máximo tanto para los resultados en el que ambos cooperan como para el fraude mutuo:

[2024_06_05_C.jpg]

Es importante destacar que z no toma en consideración la eficiencia, sino solo la equidad, como podemos ver a continuación en este DP evaluado por una función de utilidad totalmente equitativa:

[012]

Los resultados más equitativos son los situados en la diagonal que va de F1 ; C1 a F5 ; C5. Obviamente, en términos objetivos este último resultado es mucho peor para ambos jugadores que el primero. Sin embargo, vemos que todos los resultados de la diagonal, evaluados con w = 1 (α = 0, β = 0, γ =1), obtienen siempre el máximo valor en la escala 0 – 1. Otras distribuciones de α, β y γ (Ego, Alter, Equity) producen funciones de utilidad con un mejor ajuste entre equidad y eficiencia.

Esta proporcionalidad entre equidad y eficiencia se alcanza también calculando el producto de Nash (Nash product), empleado originalmente para hallar el equilibrio de un juego de negociación no cooperativo entre dos jugadores. Aunque no es un principio orientado por una concepción de justicia, proporciona resultados que concuerdan con ciertas intuiciones morales acerca de lo justo o equitativo. En esta simulación, el producto de Nash no está contemplado entre las operaciones que se pueden efectuar con los pagos.

Resumen

* Por un lado, tenemos tres variables, p_p, p_a y z, que representan, respectivamente, los pagos materiales del propio jugador que estemos considerando, los pagos del otro jugador y una cierta relación entre ambos pagos.

* Por otro, α , β y γ son los pesos relativos que el jugador asigna a p_p, p_a y z.

* Así, podemos llamar a α “índice de egoísmo”, a β “índice de altruismo” y a γ “índice de equidad”. Podemos decir que p_p, p_a y z son valores objetivos, mientras que α, β y γ son subjetivos.

* Una serie de operaciones sobre estas seis magnitudes arrojan un resultado que podemos denominar “utilidad”, ya que sitúan cada estado de cosas en un orden de preferencias en una escala que va de 1 a 0.

En un primer momento, esta utilidad se mide en la misma escala que los pagos materiales (Matrix 0), pero posteriormente sufren dos transformaciones de las que resultan los pagos subjetivos de Matrix 1, 2 y 3. Estas transformaciones son: 1) paso de utilidad cardinal a utilidad ordinal, y 2) reducción de la escala ordinal a un rango que va de 1 a 0.

1)  Paso de utilidad cardinal a ordinal. Este es un tema habitual en teoría de juegos. La utilidad cardinal representa el hecho intuitivamente aceptable de que las preferencias, además de un orden, tienen una intensidad. Sin embargo, en esta simulación me valdré sólo de escalas ordinales, ya que éstas permiten a los agentes reconocer tipos de juegos por la estructura de relaciones de preferencias (propias y ajenas) y no por los pagos materiales. El dilema del prisionero, por ejemplo, queda definido por ciertas relaciones entre sus resultados: así, el mejor resultado de un jugador es el peor para el otro; si ambos intentan maximizar su utilidad, obtendrán sus segundos peores resultados; y si ambos renuncian a maximizar obtendrán sus segundos mejores resultados.

Tomemos este juego:

Y este otro:

Aunque los pagos son diferentes en cada juego, el tipo de situación es la misma. Es más, los pagos no sólo son diferentes, sino que en el segundo juego son asimétricos entre ambos jugadores. Aún así, el orden de las preferencias se mantiene constante:

2) Conversión de los pagos ordinales a la escala de 0 – 1. Si la primera conversión sirve para reconocer un mismo juego con diferentes pagos, esta segunda permitirá evaluar de manera consistente juegos con diferentes cantidades de resultados. En los ejemplos que acabamos de ver hay cuatro posibles resultados, pero en un juego de 5 × 5 los resultados pueden ser hasta 25 (un juego de n × n podría tener menos de n × n resultados diferentes, si algunos son idénticos). Al reducir los pagos a una escala de 0 (menos preferido) a 1 (más preferido) cualquier función de utilidad se puede aplicar como una regla uniforme para evaluar diferentes tipos de juego.

            Por ejemplo, si hay cuatro resultados posibles diferentes, se les asigna, de menos a más preferidos, los valores 0, 0.33, 0.67 y 1. Si los posibles resultados fuesen cinco diferentes, tendrían los valores 0, 0.25, 0.5, 0.75 y 1.

  

  

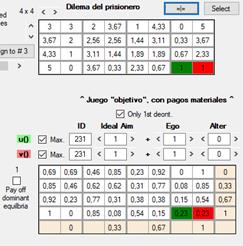
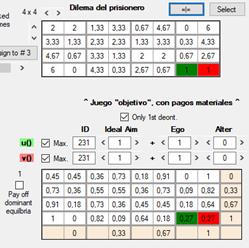
[013]
Estas imágenes son de una versión previa. La única diferencia son los rótulos u() y v(), que ahora son uF, vF, uC y vC.

            En estos ejemplos de dilema del prisionero, vemos que los resultados extremos, cooperar y ser defraudado, por un lado, y defraudar a quien coopera, por otro, se mantienen constantes como 0 y 1. Los resultados de la cooperación mutua son los que mas varían, entre 0.43 y 0.71, mientras que el rango para el resultado del fraude mutuo está entre 0.23 y 0.33.

            Pese a estas divergencias, las preferencias expresadas con pagos ordinales permiten evaluar con criterios uniformes una variedad de juegos diferentes, a diferencia de las simulaciones más habituales, que fijan uno o unos pocos juegos y una interpretación previa de qué opciones son cooperativas o defectivas (por ejemplo, que la fila superior es cooperar y la fila inferior defraudar).

            Probemos, por ejemplo, la función de utilidad w = 181 (0.55 egoísmo, 0.2 altruismo y 0.25 equidad). La evaluación que esta función hace de los resultados en todos los juegos de la lista se ajusta a nuestras intuiciones racionales y morales. Veamos tres ejemplos.

[014]

Obsérvese que se marcan en verde y rojo los pagos de los resultados que de hecho se han producido, pero si atendemos a los pagos de Matrix 3 vemos que F1 = 1 ; C1 = 1, es decir, que w 181 asigna la valoración máxima al resultado de la mutua cooperación.

            El siguiente ejemplo es el juego de partir la tarta:

[015]

Este ejemplo nos sirve también para ver el caso de juegos con varios equilibrios: aquí, todos los marcados en verde y rojo. En estas situaciones, la teoría prescribe que debería emplearse una estrategia mixta, eligiendo al azar una estrategia según una cierta distribución de probabilidades que dejen indiferente al otro jugador, en el sentido de que la utilidad esperada de todas sus estrategias sea la misma. En esta simulación, se selecciona una estrategia al azar, pero con una distribución equiprobable de las mismas, lo cual se desvía de la ortodoxia; espero poder justificar más adelante esta implementación.

            Retomando el análisis de cómo se valoran los resultados, vemos que w 181 señala F3 = 1 ; C3 = 1 como el mejor resultado posible, es decir, el que se deriva de que ambos jugadores hayan pedido la mitad de la tarta.

            El siguiente ejemplo es el juego del ultimátum:

[016]

 

Aquí, el resultado mejor valorado es F3 = 1 ; C1 = 1, es decir, jF hace una propuesta equitativa y jC la acepta.

            Algunas otras funciones con índices α, β y γ similares podrían producir resultados parecidos; todo es cuestión de probar. Sin embargo, lo más interesante será poner en marcha la simulación en un mundo poblado de agentes con funciones de utilidad completamente aleatorias para ver cuáles son las más favorecidas por la selección natural. Ya puedo anticipar que a meundo las funciones más exitosas incorporadas en el genoma de los agentes artificiales distarán mucho de concordar con nuestras intuiciones morales o racionales. Creo que la principal aportación de mi simulación tiene un carácter negativo: mostrar que este tipo de modelos son muy sensibles al grado de plausibilidad que el experimentador concede a ciertos supuestos iniciales, por lo general muy simplificados. Un modelo, ciertamente, debe ser lo más simple posible, pero conviene tener a la vista lo que ocurre a medida que el modelo va ganando en complejidad o, dentro de un mismo grado de simplicidad, cuando se modifican ligeramente las condiciones iniciales.

            Además de las funciones numeradas del 1 al 231, resultantes de las diversas combinaciones de α, β y γ, hay otras 231, numeradas del 232 al 462, exactamente iguales a las de la primera serie, pero con con signo negativo. Tomemos un juego con la función de utilidad egoísta que ya conocemos (231):

[017]

La correspondiente función negativa permite invertir totalmente la “percepción” de los resultados, haciendo que lo más prefereible pase a ser lo menos preferible, o viceversa:

 

[018]

     Para cambiar el signo de la función basta con hacer click sobre él.

         Las funciones de utilidad positivas están seleccionadas por defecto en la pantalla incial, pero cuando iniciemos una simulación en el mundo virtual podrán ser generadas al azar con igual probabilidad para cualquier “gen” en el genoma de los individuos. Las funciones de utilidad negativas sirven para representar disposiciones sádicas, envidiosas, masoquistas o que simplemente buscan castigar. Así, por ejemplo, tras convertir los pagos ordinales a la escala 0 – 1, una función envidiosa o vengativa asignará 0 al pago más alto del otro jugador y 1 a su pago más bajo. Conviene no perder de vista que tanto altruistas como sádicos se interesan profundamente por las preferencias del prójimo, si bien los sádicos procuran que no se realicen, es decir, minimizan la que consideran que es la utilidad del otro jugador. En rigor, siguen siendo estrategias maximizadoras, sólo que buscan maximizar otra función de utilidad.

         El conjunto de funciones de utilidad, U, puede verse también como una función que, a su vez, toma como argumento la evaluación de las acciones de otro jugador y da como resultado una función de utilidad u(p_p, p_a). Pero lo cierto es que en U, el continuo* 0 – 1 del eje X no corresponde necesariamente a una mayor o menor inclinación a nada. Simplemente es una colección de “zonas de respuesta”, en principio sin continuidad alguna. Llegado el caso podrían contener funciones de utilidad ordenadas de manera progresiva, y entonces el continuo de la evaluación sí representaría una tendencia, pero, en general, pueden ser valores completamente discontinuos. En este sentido, no conviene considerar a U y a V como funciones.
          * Aunque el resultado x de una evalación está en el continuo 0 – 1, x se redondea a un decimal, de lo cual resultan 11 posibles valores discretos (0, 0.1, ..., 0.9, 1), cada uno de los cuales corresponde a una función de utilidad en el conjunto U.

          Los conjuntos U y V son parte de lo que consideraemos el genoma de un jugador, para acceder al cual primero haremos en el botón World. Se abrirá la ventana con el mapa del mundo, donde seleccionaremos un agente en el mapa haciendo clic sobre él y, a continuación, clic en el botón Genome. Aparecerá entonces la pantalla de edición del genoma.

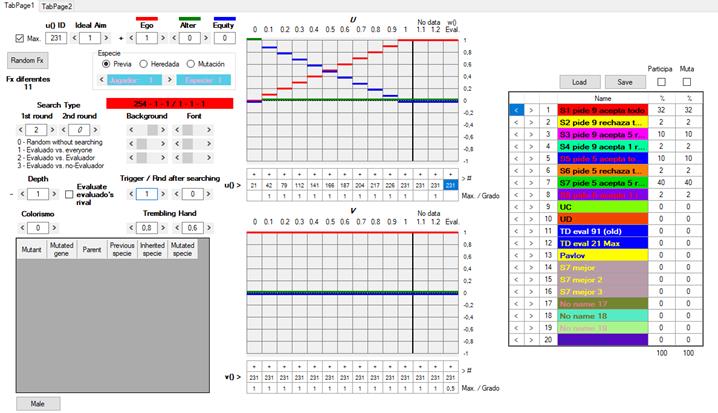
[Figura 19]

En el centro hay dos tablas. La superior representa el conjunto U y la inferior, el conjunto V. Para este ejemplo he escogido uno de los inusuales casos en los que puede reconocerse una regularidad o continuidad en las funciones de U. Se trata de un conjunto elaborado deliberadamente por el usuario, pero lo habitual es que la ventana de edición del genoma presente un aspecto más parecido a esto:

 

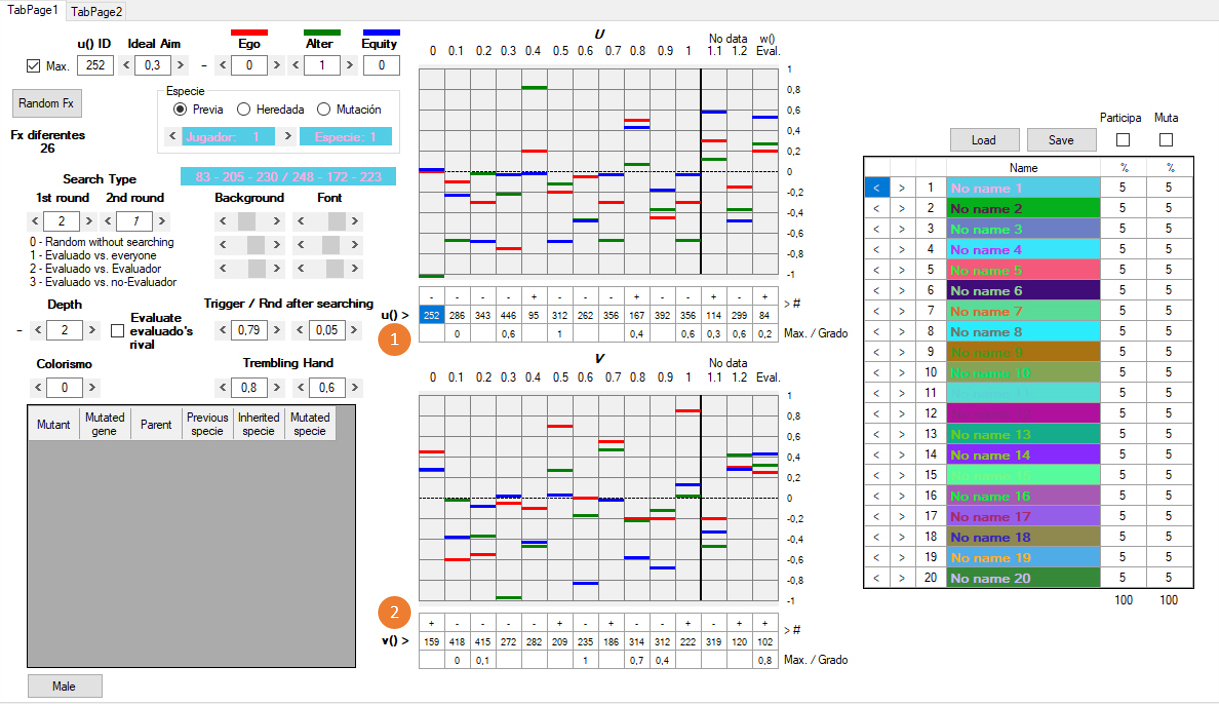
[Figura 20]

            Al iniciar una simulación, U y V, y el genoma completo, están generados al azar. Sin embargo, el usuario puede acotar los márgenes de los valores que se generarán al azar (cfr. Infra X) [Esto se queda sin explicar por ahora]. Lo llamo “genoma” porque contiene todas las variables que determinan el modo en que un jugador examina a otros, cómo toma sus decisiones y qué fenotipo tiene (colores), variables éstas que se transmiten por herencia a otros individuos (o por imitación, según se quiera interpretar el modelo).

            En el eje X de los conjuntos U y V se sitúa el valor e que un jugador J1 (ya sea jF o Jc) asigna a la conducta observada del otro jugador, J2, con quien va a interactuar. Aunque en el caso ideal sería un continuo, para simplificar los cálculos y acelerar la ejecución del programa, X está seccionado en 11 posiciones discretas que van de 0 a 1 en intervalos de 0.1 (s₀, ..., s₁₀). En las filas rotuladas como u() y v() [1] y [2], un valor discreto entre 1 y 462 indica, para cada s, qué funciones de utilidad empleará J1 para configurar, a partir de los pagos materiales del juego original, el juego subjetivo en el que tomará una decisión. Como puede observarse, las funciones comprendidas 1 y 231 tienen encima un signo positivo, y las que van de 232 a 462, uno negativo.

            J1 es el jugador cuya acción vamos a estudiar, y J2 es el jugador con el que interactúa J1. Durante la simulación, cada vez que un jugador (J1) toma un decisión frente a otro jugador (J2) sigue una serie de pasos que se indican a continuación. En la ejecución de dichos pasos intervienen una serie de “genes”, cuyos rótulos se indican en negrita, tal como aparecen en el editor de genomas:

1) J1 observa las conductas anteriores de J2. Puede observar entre 1 y 8 jugadas (Depth), comenzando desde la primera de J2 y avanzando hacia la más reciente [+] o, al revés, comenzando por la jugada más reciente de J2 y retrocediendo hacia la primera [-]. Cuántas jugadas puede llegar a observar viene determinado por tipo de búsqueda (Search Type):

1.1) Tipo 0 – Doesn’t search: no busca ninguna jugada y elige al azar una de sus 11 funciones u y la correspondiente v que le atribuye a J2.

1.2) Tipo 1 – Evaluado vs. everyone: busca jugadas de J2 contra cualquier jugador, ya sea el propio J1 o terceros (J3).

1.3) Tipo 2 – Evaluado vs. Evaluador: busca jugadas de J2 contra J1.

1.4) Tipo 3 – Evaluado vs. no-Evaluador: busca jugadas de J2 contra terceros (J3).

El “evaluador” es J1, el “evaluado” es J2, el “no-evaluador” es cualquier otro jugador (J3) diferente de J1 que ha jugado contra J2 y “everyone” es J1 y todos los J3.

La búsqueda se realiza en dos fases. Si en la primera búsqueda no encuentra suficientes interacciones que satisfagan el primer criterio de búsqueda, puede seguir buscando según un segundo criterio.

 

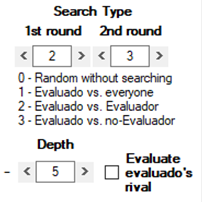
La aplicación de un segundo criterio sólo ocurre cuando el primer criterio de búsqueda es del tipo 2 o 3. Por ejemplo: supongamos que J1 quiere examinar 7 jugadas de J2 contra el propio J1 [Search Type 2], pero J1 y J2 sólo han interactuado 4 veces hasta el momento. Entonces J1 puede buscar 3 jugadas más en las que J2 haya interactuado contra otros jugadores (J3) [Search Type 3].

            Cuando el tipo de búsqueda aparece en cursiva, significa que ese criterio no se puede aplicar. Por ejemplo, si el primer criterio es del tipo 2, el segundo no puede ser también del tipo 2, ya que recogidas una serie de interacciones con el tipo 2, al aplicar de nuevo el mismo criterio repetiría la serie de interacciones que ya ha observado. En estos casos, J1 se conforma con los datos obtenidos, aunque no sean todos los que esperaba recabar.

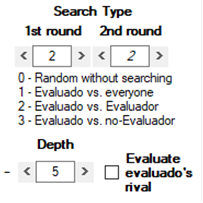
1.5) Por otra parte, si está marcada la casilla Evaluate evaluado’s rival, J1 no evalúa lo que ha hecho J2, sino lo que el rival de J2 ha hecho contra J2 en una determinada interacción. Entre otras cosas, esto puede propiciar que J1 se evalúe a sí mismo, cuando J1 ha jugado con J2. Así, con Search Type 2 = Evaluado vs. Evaluador, J1 evalúa a J2, pero si está marcada la casilla Evaluate evaluado’s rival, J1 evalúa el movimiento del rival de J2, que no es otro que él mismo, J1.

2) Cada uno de los n movimientos observados (entre 1 y 8) los evalúa J1 con una función de utilidad,
w(p_p,p_a), semejante a las funciones del tipo u y v. Los argumentos p_p y p_a son los pagos materiales que J1 y J2 han obtenido del juego original. Para cada resultado, w arroja un valor y_n entre 0 y 1. De los n movimientos observados y evaluados se calcula el promedio de los valores y₁ + y₂ + ... + y₈, que da la evaluación general e de la conducta observada en J2.

2.1) La media e de los n movimientos evaluados se redondea a un número de un solo decimal entre 0 y 1, que determina qué funciones de los conjuntos U y V se adoptarán para tomar la decisión.

2.2) Cada genoma tiene definidos dos márgenes de valores tales que, si y_n está dentro de sus límites, J1 da una respuesta especial. Pese a su carácter ad hoc, estas dos respuestas especiales son necesarias para simular cierto tipo de estrategias muy estudiadas en la literatura y empleadas en otras simulaciones.

2.2.1) La primera de estas respuestas es conocida como “Trigger”: una vez hallada una jugada n de J2 cuyo valor de y_n está dentro del margen especificado, deja de buscar más jugadas y considera sólo y_n para dar una respuesta, sin buscar la media e a partir de un conjunto de jugadas. Por ejemplo, veamos el caso de J1 = 696, con estos márgenes para Trigger:

A continuación vamos a ver los dos historiales de interacciones que se encuentran a la izquierda en la ventana del mundo. El de arriba muestra todas las jugadas de un cierto jugador, en nuestro caso J1 = 349, contra todos los jugadores con los que ha interactuado en una generación.

Si hacemos click sobre el número 9 de la primera columna del historial superior, se mostrará en el historial inferior la lista de interacciones de J2 = 317. En este ejemplo J1 está programado por sus “genes” para mirar las 8 primeras jugadas de J2 contra cualquier jugador que no sea J1. Cumpliendo estos requisitos, observa las jugadas 3, 4, 5, 6 y 7. Aquí, aunque sólo ha observado cinco, detiene la búsqueda, ya que da un valor de 1 a esta quinta interacción de J2, y dado que 1 está en el intervalo 0.6 – 1, sólo atiende a este último resultado. En azul claro quedan marcados los 4 primeros resultados a los que estaba prestando atención y en morado el que ha causado la respuesta especial (trigger). En la primera fila de la tercera tabla, este resultado definitivo queda indicado entre paréntesis invertidos: )1(.

 

[Figura 24]

Aquí podemos ver el genoma completo de J1:

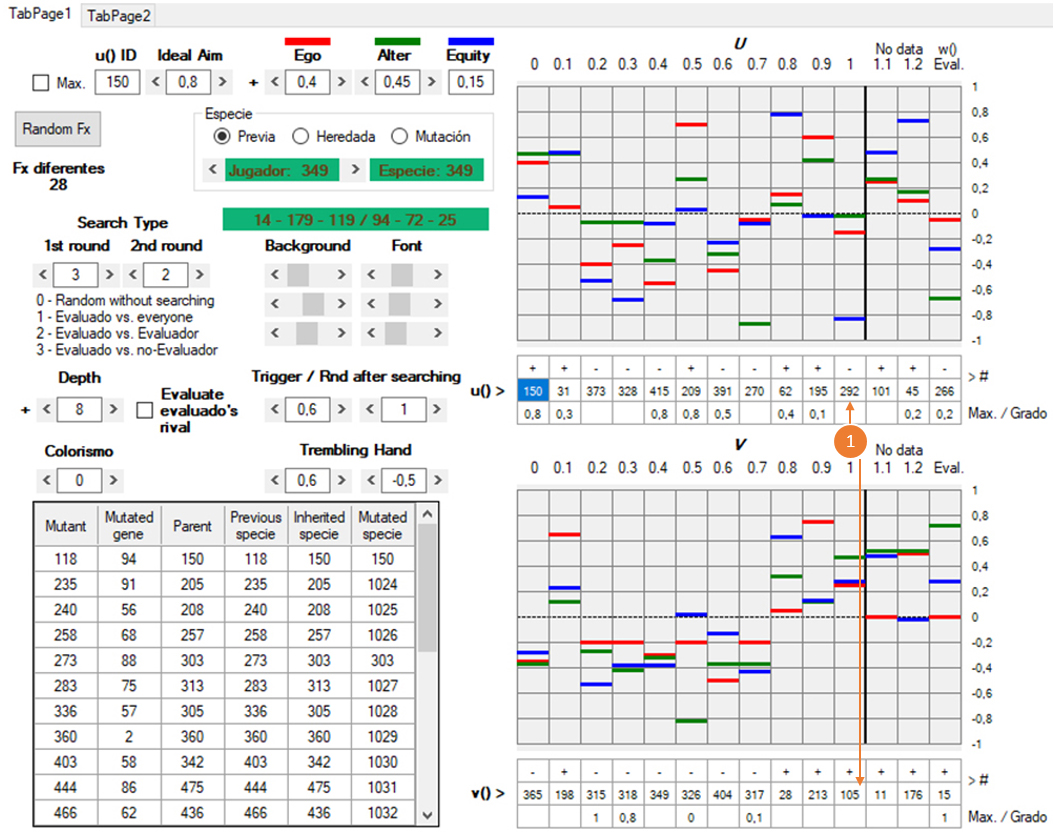
[Figura 25]

En la posición 1 [1] de U tiene u = 292 y en la posición 1 de V, v = 105. Si volvemos a mirar el historial superior de la figura 24, vemos que en las columnas 5 y 7 de la novena fila [1] aparecen precisamente esas cifras, que indican en el historial cuáles son las funciones de utilidad empleadas para definir la decisión que toma J1 contra J2 en esa interacción.

[En sentido estricto, la respuesta “trigger” que repite indefinidamente su respuesta al identificar una determinada conducta sólo se verifica en búsquedas ascendentes.]

2.2.2) El segundo tipo de respuesta especial es al azar, pero, a diferencia del tipo de búsqueda 0 (cfr. Supra 1.1), no es una decisión aleatoria absoluta que ignora todo movimiento observado de J2, sino que es una respuesta al azar para un cierto rango de e. El rango será el comprendido entre los mismos márgenes que se usan para causar “trigger”, pero tomando el margen superior como margen inferior y viceversa.

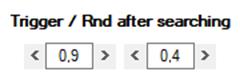
Estos márgenes no pueden generar “trigger” porque nunca será el caso que y sea mayor que 0.9 y menor que 0.4. Pero si e está entre 0.4 y 0.9, J1 no responderá con el par u v que corresponda a e, sino que escogerá al azar una de las 11 posiciones de U y V. Llamaremos “azar condicionado” a este segundo tipo de respuestas ad hoc.

Tres notas:

2.2.2.1) Obsérvese que trigger detiene su búsqueda al encontrar un valor de y en el rango especificado, sin llegar a calcular e, mientras que el azar condicionado intenta agotar su búsqueda, calcula e y comprueba si se encuentra en el rango.

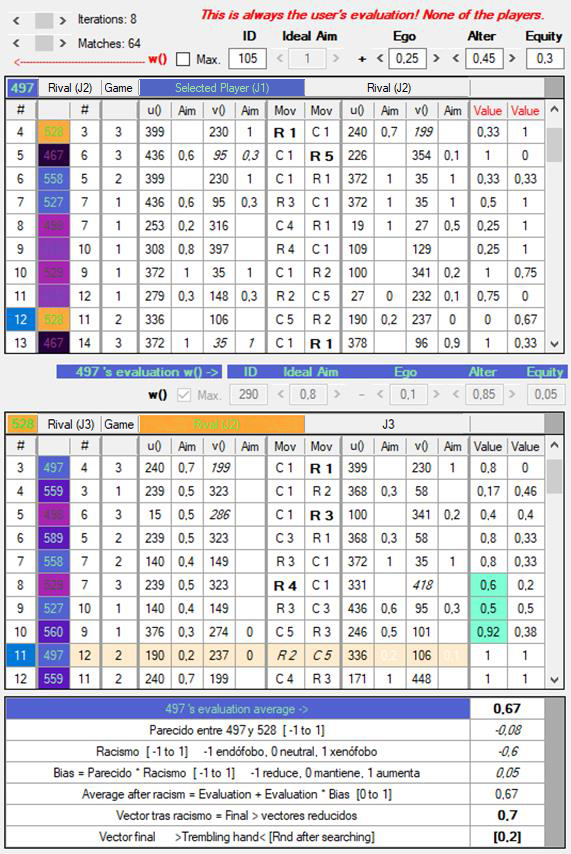
[Figura 26]

2.2.2.2) Al igual que el azar absoluto (1.1), el resultado se indica entre corchetes, pero ahora en la última línea de la tabla de promedios (la tercera en el grupo de los historiales).

2.2.2.3) Para que el azar condicionado pueda tener lugar, tiene que estar marcada la casilla que lleva su nombre:

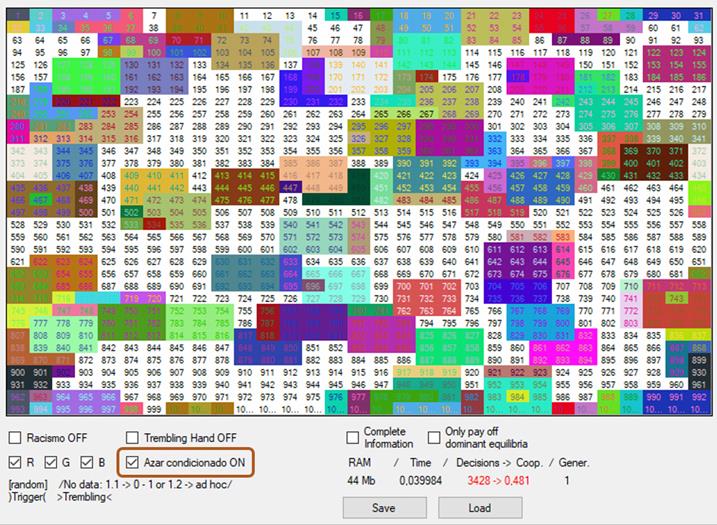
[Figura 27]

2.3) Si se han agotado las búsquedas de los tipos 1, 2 o 3 sin obtener resultados que se ajusten a alguno de los criterios, entonces se toman las funciones u y v de la columna señalada como No data 1.1 [1]:

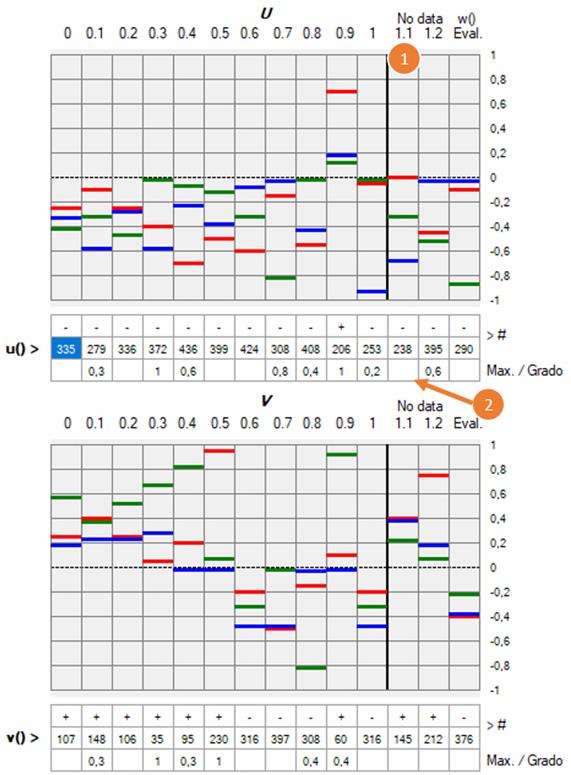
[Figura 28]

          En dicha columna vemos que u₁₁ = 238 y v₁₁ = 145; en la última fila (Max./Grado) hay una casilla en blanco [2], la cual, al igual que otras casillas en esa fila, podría contener también un número entre 0 y 1.

2.3.1) Si en la posición 11 la casilla Max./Grado está en blanco, las u y v finalmente seleccionadas serán las de la columna No data 1.2, que en este ejemplo son u₁₂ = 395 y v₁₂ = 212. En la primera fila de la tabla de promedios, esta selección final se indica entre barras inclinadas /1.2/:

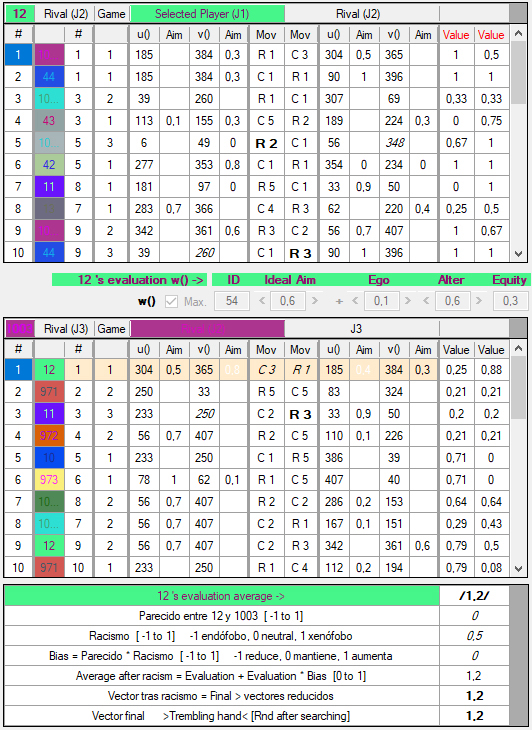
[Figura 29]

En general, se indicará entre barras inclinadas, / /, toda referencia a una función de utilidad para cuya determinación no se ha encontrado ninguna interacción previa.

2.3.2) Si la casilla Max./Grado de u₁₁ no está vacía, el número indica cuál de los 11 pares de funciones (u₀ – u_10, v₀ – v₁₀) será seleccionado:

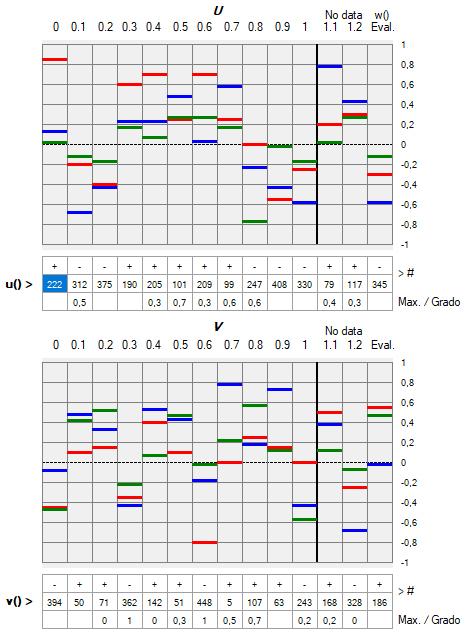
[Figura 30]

En este ejemplo, el valor es 0.4, de manera que las funciones empleadas serán u₄ = 205 y v₄ = 142. En la tabla de promedios, este valor final también se representa entre barras inclinadas, /0.4/.

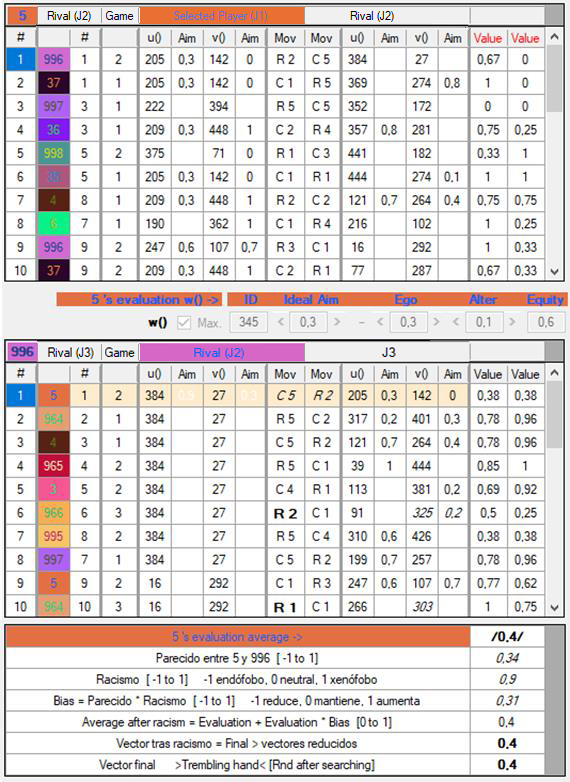
[Figura 31]

Resumen:

a) Entre barras inclinadas deberían mostrarse valores entre 0 y 1, en intervalos de 0.1, o bien 1.2. Si en algún caso apareciese /1.1/, esto sería un bug muy significativo que agradecería se reportase.

b) Hay dos maneras de determinar una función ad hoc cuando J1 no cuenta con ningún elemento de juicio para evaluar la conducta de J2.

Aunque las dos son respuestas ad hoc, cuando la función de la posición 1.1 remite a la posición 1.2, este carácter arbitrario es aún más marcado, ya que la posición 1.2 está totalmente desligada del continuo 0 – 1 de U. Esta ligera irregularidad habilita la existencia de estrategias lo suficientemente flexibles para reproducir simulaciones de juegos como el ultimátum.

Resumen

El algoritmo para la toma de decisiones puede esquematizarse del siguiente modo:
Observar 1 – 8 movimientos → Evaluar cada movimiento con w en una escala de 0 a 1 → Obtener la media e de la serie de evaluaciones, redondeada a décimas (0, 0.1, 0.2, ... , 1.0) → Ver qué funciones u (propia) y v (ajena) corresponden a e en U y V  → De aquí resulta una matriz de pagos sobre la que se toma la decisión.

Me referiré como “estrategia” al genoma que determina todos estos pasos, así como al propio procedimiento en su ejecuión. Cuando emplee el término “estrategia” en el sentido habitual que tiene en teoría de juegos, como “curso de acción”, lo indicaré explícitamente.

Estrategias maximizadoras vs. deontológicas

            Los agentes vistos hasta ahora son puramente prudenciales, es decir, que intentan maximizar una cierta función de utilidad. Si bien esto es lo habitual en teoría de juegos, la presente simulación incluye también funciones de utilidad que denominaré deontológicas. Para explicar este concepto, lo más importante será diferenciarlo de las funciones maximizadoras y mostrar su relevancia operativa. Comenzaremos por notar que la noción de elección racional como maximización de la utilidad, al igual que toda definición, tiene un componente tautológico, que, sin embargo, no menoscaba la teoría. Análogamente, y partiendo de la utilidad como medida de la preferencia, entenderemos que una función de utilidad deontológica es aquella que coloca en el primer lugar de sus preferencias una cierta acción que ha de hacerse por deber. Para dar un contenido a esta expresión, habrá que analizar y comparar cómo funcionan en la simulación los algoritmos de ambos tipos de función de utilidad.

            Cuando J1 emplea una estrategia maximizadora, busca maximizar una función de utilidad dada, u, teniendo en cuenta lo que cree que hará J2 (o lo que sabe que ha hecho, en juegos sucesivos) en su intento de maximizar otra función de utilidad v. Esta situación estratégica supone el caso más común en teoría de juegos. Por otra parte, lo fundamental en el concepto de función deontológica es que el agente o algoritmo que la emplea actúa sin atender a consideraciones prudenciales acerca de lo que espera que de hecho ocurra o haya ocurrido. Sigue habiendo una función u que, al transformar en pagos subjetivos los pagos materiales de un juego objetivo, configura la matriz de pagos sobre la que se toma la decisión. Sin embargo, el resultado que maximiza u es ahora un valor más dentro de un espectro, y no representa necesariamente lo que la estrategia va a elegir; podemos decir que es un fin posible. En el otro extremo de los fines posibles estaría la minimización de u, pasando por una serie de puntos intermedios, todos los cuales pueden llegar a ser el objetivo al que aspira (Aim) J1.

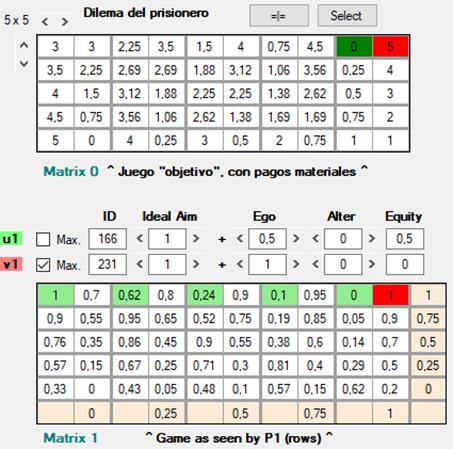
[Figura 32]

         Las acciones en sí mismas, y no los resultados, son lo que una función deontológica ordena en una escala de preferencias. Los valores ordinales asignados a cada acción se muestran en color beige, en la columna del extremo derecho para jF y en la fila inferior para jC. Así, para jF la acción más valiosa es F1 = 1, seguida de F2 = 0.75, hasta llegar a la menos valiosa, F5 = 0 (las acciones como objeto de preferencias las escribo en cursiva). Ahora cabe pregutarse por qué ciertas acciones son más valiosas que otras. La respuesta es que sigue habiendo un vínculo con los resultados, aunque, como buenos kantianos, diremos que son resultados a los que se llegaría si todo el mundo siguiese un cierto principio (el mandato de la ley moral), incluso aunque “no haya habido nunca acciones emanadas de esas puras fuentes [de la moralidad], que no se trata aquí de si sucede esto o aquello, sino que la razón [...] ordena lo que debe suceder y que algunas acciones, de las que el mundo quizá no ha dado todavía ningún ejemplo y hasta de cuya realizabilidad pueda dudar muy mucho quien todo lo funde en la experiencia, son ineludiblemente mandadas por la razón.” Fundamentación de la metafísica de las costumbres, (p. 39)

            Para jF, F1 = 1 es la acción más valiosa porque conduciría al resultado F1 = 1 ; C1 = 1 si jC siguiese también el mismo principio. El caso es que jF cuenta con que jC, aplicando la función maximizadora v = 231, escogerá C5 y, sin embargo, pese a que jF sabe lo mucho que le perjudicará F1 = 0 ; C5 = 5, elige F1. Las acciones seleccionadas por una función deontológica quedan señaladas por casillas en tonos verde o rojo más claros, mientras que el resultado que espera obtener una función maximizadora se indica con el habitual verde o rojo más oscuros.

            Ahora bien, los agentes artificiales se alejan de una concepción kantiana estricta en dos aspectos:

            1) No hay una única ley moral reconocida por todos: en el caso que nos ocupa, jF estaría haciendo universal el principio u = 166, pero podría ser cualquier otra función de utilidad.

            2) Cada uno de esos principios admiten también grados de cumplimiento. Dada una función de utilidad, todas las acciones se ordenan según el mejor resultado posible que podrían llegar a generar. En el ejemplo de la figura 32, para jF están todos en la columna 1, y van desde F1 = 1 hasta F5 = 0.33.

            En último término, siempre podremos decir que sí existe un único principio moral universal, y que simplemente hay una multitud de estrategias cuyo razón práctica discurre mal, erradas en el reconocimiento de lo que ordena el imperativo categórico.

            Pese a todo, lo relevante para la simulación es la permanencia del rasgo distintivo que diferencia a las funciones deontológicas de las maximizadoras: son insensibles a la prudencia, a que el resultado fáctico o previsible frustre los fines de una ley universal, y se ciñen férreamente a la acción que, por el principio que fuese, consideran valiosa.

            Fundamentación de la metafísica de las costumbres, (p. 49) “[El imperativo de la moralidad] no se refiere [...] a lo que de ésta ha de suceder, sino a la forma y al principio de donde ella sucede, y lo esencialmente bueno de la acción consiste en el ánimo que a ella lleva, sea el éxito el que fuere.” (La cursiva es mía).

            Una multiplicidad de principios, ¿no podría ser también un modelo de una ética de las virtudes? O tal vez de la inquietante hipótesis (no aplicable al hombre, según Kant) de una suerte de voluntad diabólica:
“[...] una Razón que libera de la ley moral, una razón en cierto modo maliciosa (una voluntad absolutamente mala) [... por la que] el antagonismo frente a la ley sería elevado incluso al rango de motivo impulsor (ya que sin ningún motivo impulsor no puede el albedrío ser determinado) [...] haría del sujeto un ser diabólico.” (La religión dentro de los límites de la mera razón, pp. 44 – 45).

            Cierro aquí esta digresión acerca de las posibles interpretaciones del modelo según teorías morales conocidas, que sólo pretendía ilustrar cómo operan los algoritmos de la simulación.

            La denominación “ideal aim” denota el caso ideal que buscaría el jugador, constreñido a un cierto grado de cumplimiento del principio que esté adoptando. Cuando tal fin no es posible, la estrategia busca la mejor aproximación.

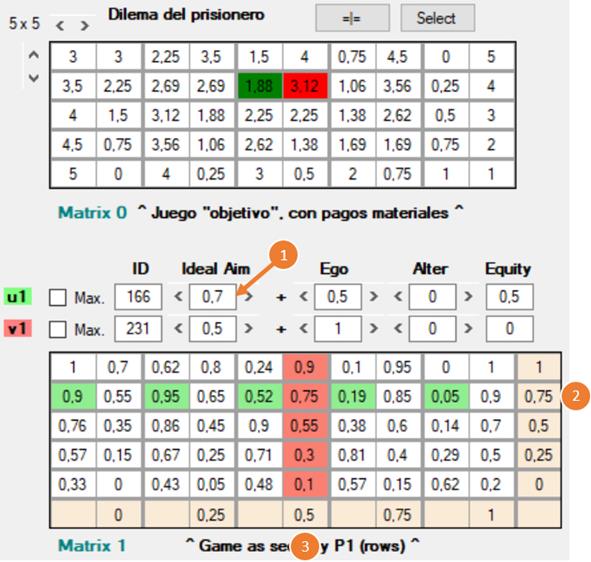
[Figura 33]

            En la figura 33, jF entiende que su deber es alcanzar el punto 0.7 [1] en la escala que ordena el valor de las acciones (columna más a la derecha, en color beige) según u = 166. Como en ella no existe tal punto discreto, opta por F2, la acción que conduce a la mejor aproximación: 0.75 [2]. Por otra parte, jF cree o sabe que jC emplea una variedad de la función deontológica v = 231 que procura alcanzar 0.5, un punto en la escala que de hecho sí está disponible [3].

            Es fundamental entender lo siguiente. Los pagos de Matrix 1 proceden originalmente de una función de utilidad que ordena los pagos de Matrix 0, pero si nos situamos en el marco más convencional de la teoría de juegos, al hablar de grados de cumplimiento, los valores de la columna en el extremo derecho de Matrix 1 quedan reducidos a una mera etiqueta cualitativa para diferentes cursos de acción: los valores de 0 a 1 ya no representan un orden de preferencias. Para llegar a esta conclusión, pensemos que, por definición, 1 es preferible a 0, pero si consideramos la tautológica doctrina de la preferencia revelada en la elección, al curso de acción escogido siempre se le podrá asignar un valor de 1 en la escala ordinal y 0 a todos los demás; y, sin embargo, la estrategia puede llegar a elegir (ideal aim) el curso de acción etiquetado como 0 o, en general, cualquier otro inferior a 1.

            Qué sentido pueda tener esto queda sujeto a interpretación del usuario. Es una opción que ofrece la simulación, pero no hay por qué emplearla. Por ejemplo, que un agente pueda escoger una acción inferior a la primera en su orden de preferencias sirve para representar conductas de castigo en diversos grados, de manera semejante a las funciones de utilidad negativas que buscan minimizar la utilidad de otro jugador (cfr. supra x).

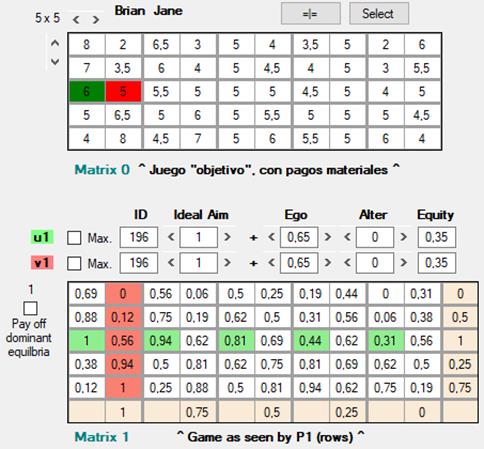
            Tenemos, pues, que el valor que jF asigna a una acción proviene de algún principio que jF juzga universal, un principio que todo el mundo debería seguir, es decir, que también jC debería hacerlo suyo. Ahora bien, parece que en determinadas situaciones hay principios que no permiten un análisis universalista. Consideremos el juego que llamaré Brian y Jane, inspirado en una situación que presenta Gauthier en Egoísmo, moralidad y sociedad liberal (p. 77):

 

[Figura 34]

            Aplicando el “principio” u = 196, la acción que jF mejor valora es F3, ya que conduciría al resultado F3 ; C1 si jC también siguiera dicho principio. Lo cierto es que en esta representación jC así lo hace, y de hecho escoge una acción, C1, que conduce al resultado F3 ; C1. Sin embargo, se trata de una mera casualidad, ya que si bien jC sitúa a C1 en el primer lugar de sus preferencias, el motivo subyacente es que conduciría a F5 ; C1, resultado éste que se alcanzaría si jF escogiese F5. Se da, pues, la paradoja de que para jC la consecución de un resultado ordenado por un cierto principio (u = 196 / Aim = 1) requeriría que jF aplicase un principio ligeramente diferente: u = 196 / Aim = 0.75. Esta esta anomalía tiene dos causas: la asimetría del propio juego y el considerable componente egoísta (0.65) de u = 196. Esta función deontológica aplicada a un juego simétrico, o el mismo juego original transformado con funciones menos egoístas (por ejemplo u = 154), conduce a resultados racionalizables en términos universalistas.

 

Selección de equilibrios

            Me ocuparé ahora del problema de la selección de equilibrios, tema sobre el que abunda literatura y que requiere varias aclaraciones en este manual.

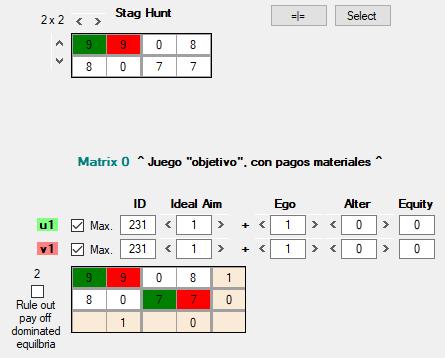
            Comencemos con el juego de la caza del venado:

[Figura 35]

            Este juego tiene dos equilibrios: F1 ; C1 y F2 ; C2. El primero sería un equilibrio dominante en términos de pagos (payoff dominant), ya que es un óptimo de Pareto en relación con todos los demás equilibrios de Nash que presenta el juego [“is Pareto superior to all other Nash equilibria in the game”]. Se lo podría ver también como el resultado de aplicar la regla de elección MaxiMax. El segundo equilibrio es dominante en términos de riesgo (risk dominant), ya que es más seguro (“less risky”, wikipedia) si el otro jugador se equivoca o se desvía [¿de qué?]. Es menos arriesgado en cuanto que proporciona mejores resultados con independencia de lo que haga el otro jugador.

            El criterio para identificar el óptimo de Pareto es claro (F1 ; C1 > F2 ; C2 para ambos jugadores) y se puede trasladar fácilmente a un algoritmo. Pero ¿cómo formalizar y programar la idea de que el otro equilibrio es “menos arriesgado” o que “proporciona mejores resultados con independencia de la elección del otro jugador”? La respuesta más inmediata estaría en la regla MaxiMin. Analicemos el razonamiento de jF (el de jC será idéntico): el mínimo posible que puede resultar de F1 es 0, y el que puede resultar de F2 es 7. Así, en el peor de los casos, F2 garantiza 7 frente 0.

            Ahora bien, si queremos guardar cierta consecuente simetría a la hora de aplicar criterios, el equilibrio dominante por pagos no se obtendría mediante la búsqueda del óptimo de Pareto, sino mediante la aplicación de la regla MaxiMax. El máximo que ofrece F1 es 9, superior al máximo que ofrece F2, que es 8.

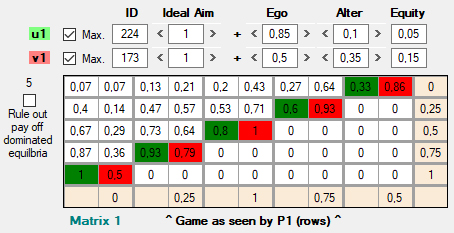
            En el juego de la caza del venado da la casualidad de que se llega al mismo resultado buscando el óptimo de Pareto y aplicando la regla MaxiMax. Pero como se ve en el siguiente ejemplo, no siempre es así:

 

[Figura 36]

            En esta situación derivada del juego partir la tarta, la regla MaxiMin elegiría F1, que garantiza 0.07, mientras que la regla MaxiMax eligiría F5, que ofrece la posibilidad (sin garantías) de obtener 1.

            Sin embargo, si el criterio de selección es buscar el óptimo de Pareto, la decisión racional no recae sobre F5 ni sobre ninguna otra acción. Sólo podemos reducir los posibles equilibrios de cinco a tres eliminando dos equilibrios (F1 ; C5 y F2 ; C4) que en términos de pagos son inferiores a los otros tres. Si marcamos la casilla Rule out pay off dominated equilibria, éste es el resultado:

 

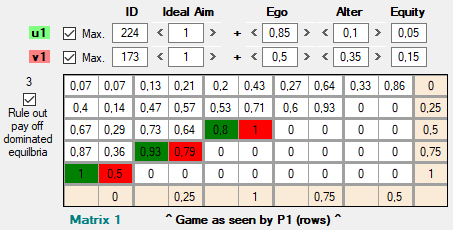
[Figura 37]

En efecto, desaparecen los equilibrios F1 ; C5 y F2 ; C4, que eran para ambos jugadores inferiores a los tres que han quedado seleccionados. Pero entre estos tres ya no hay ninguno que sea un óptimo de Pareto. Desde el punto de vista de jF, el equilibrio F5 ; C1 es dominante por pagos, el equilibrio F3 ; C3 es dominante por riesgo, y el equilibrio F4 ; C2 estaría a medio camino entre los dos.

            Ahora, para seleccionar alguno de ellos, cabría aplicar alguna de estas reglas:

            1) MaxiMax: sin implementar aún en la simulación (y engorrosa de programar).

            2) MaxiMin: ídem

            3) Maximización de la utilidad esperada, asumiendo la equiprobabilidad de las posibles acciones del otro jugador: sin implementar, pero un poco más sencilla de programar.

            4) Buscar un óptimo de Pareto (no siempre lo habrá).

            5) Escoger una acción al azar, con igualidad de probabilidades para todas (procedimiento actualmente implementado en la simulación).

            Por su carácter en apariencia arbitrario y simplista, la regla 5 requiere algún tipo de justificación. Una posible racionalización: según lo que haya escogido, y sin que nosotros podamos verlo, el jugador ha sido más o menos averso al riesgo. Si implementase las reglas 1 – 4 (cosa que haré en una futura actualización), éstas serían parte del genoma del jugador y serían visibles para el usuario. A su vez, que una de esas reglas esté incorporada a los genes de un agente es algo que en último término estará determinado al azar; no es muy diferente de elegir una acción al azar y suponer una regla subyacente que no podemos ver.

            La regla que descarta los equilibrios dominados por pagos coincide en algunos casos con la búsqueda de un óptimo de Pareto. Esta regla sí está disponible en la simulación, pudiendo el usuario elegir si será aplicable o no. Si lo es, la emplearán todos los jugadores, sean cuales fueran sus genes: se la considera parte del conocimiento común de la racionalidad de los agentes. Después de todo, ¿por qué va a pensar nadie que hay un riesgo en cazar el venado, si es conocimiento común que se trata del mejor resultado posible para todos? Los errores, la información incompleta y las manos temblorosas están incluidas en la simulación, pero en otro nivel. El problema de la selección de equilibrios se presenta en lo que llamamos “juego subjetivo”, el lugar último donde el agente toma su decisión y la teoría de juegos rige en sus aspectos más ortodoxos.

            Si salimos de este nivel y volvemos al del juego objetivo, hay una manera adicional de seleccionar uno de los equlibrios admitiendo diversos grados de riesgo, y es emplear una función de utilidad deontológica. Para este análisis vamos a partir del juego original de partir la tarta:

 

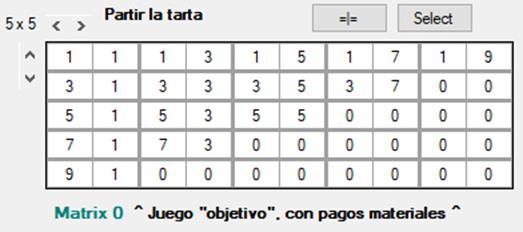
[Figura 38]

Los cinco equilibrios posibles van desde la esquina inferior izquierda (F5 = 9 ; C1 = 1) ascendiendo en diagonal hasta la esquina superior derecha (F1 = 1 ; C5 = 9). Vamos a tomar u = 224 y v = 173, como en el caso que veníamos estudiando, pero con la diferencia de que ahora u es una función deontológica. Según el grado de cumplimiento (0.6, 0.7 o 1) los equilibrios que intenta alcanzar serán diferentes:

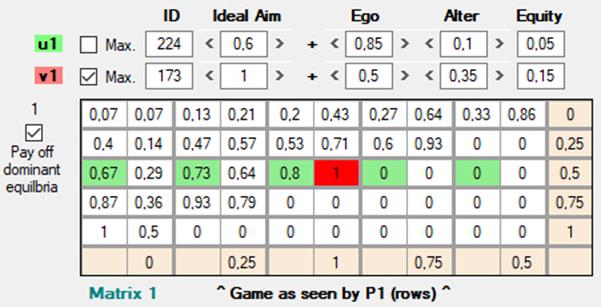
[Figura 39]

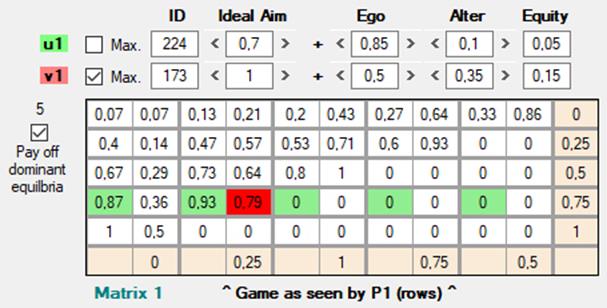
[Figura 40]

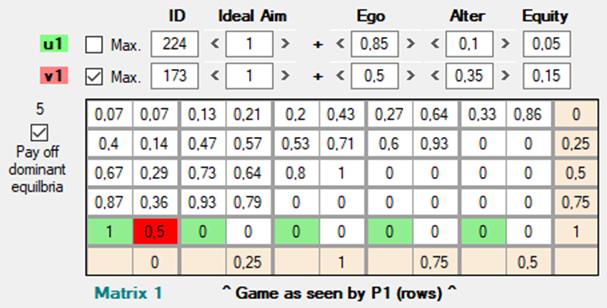
[Figura 41]

            Por último, conviene destacar que en situaciones donde no hay un único equilibrio la solución perfectamente racional consiste en emplear estrategias mixtas (en este análisis empleo "estrategia" en su sentido habitual, como "curso de acción"). Mediante una estrategia mixta, jF elige una acción al azar asignando a cada una de sus opciones disponibles una cierta probabilidad tal que la utilidad esperada para jC sea idéntica para todas las acciones de éste. Del mismo modo, las probabilidades con las que jC eligirá su acción aleatoria dejan indiferente a jF en cuanto a la utilidad esperada de sus cursos de acción. Para un juego de 2 × 2 este cálculo es bastante sencillo:

	Elige C1 con probabilidad q	Elige C2 con probabilidad 1 - q
Elige F1 con probabilidad p = 0.3	7 ; 7	3 ; 0
Elige F2 con probabilidad 1 – p = 0.7	0 ; 3	6 ; 6

          Al calcular las probabilidades  p₁ y p₂, jF busca que para jC las utilidades esperadas de C1 y C2 sean idénticas, de modo que le dé igual elegir una que otra columna.

p . 7 + (1 – p) . 3 = p. 0 + (1 – p) . 6

Si resolvemos la ecuación, tenemos que p = 0.3 y 1 – p = 0.7, de manera que las utilidades esperadas de C1 y C2 son en ambos casos 4.2. Como jC no tiene motivos para escoger una u otra, su decisión racional consitirá en emplear también una estrategia mixta que deje indiferente a jF.

            Sin embargo, para juegos con más estrategias es preciso resolver sistemas de ecuaciones de una complejidad que, si se busca cierto grado de realismo en el modelo, no cabe atribuir a un agente imperfectamente racional. A lo sumo, una capacidad de cálculo tan refinada debería ser el resultado evolutivo de generaciones de agentes más elementales cuya racionalidad se va optimizando mediante un proceso de selección natural.

 

La ventana del mundo

            Desde la ventana de inicio del programa, haciendo clic en el botón World se accede a la ventana del mundo, donde se desarrollan las simulaciones evolutivas propiamente dichas. La ventana del mundo consta de dos grandes partes: el mapa del mundo [4], a la derecha, y las tablas de historiales [1, 2 y 3] a la izquierda (la primera vez que accedemos a esta ventana, éstas se encuentran vacías).

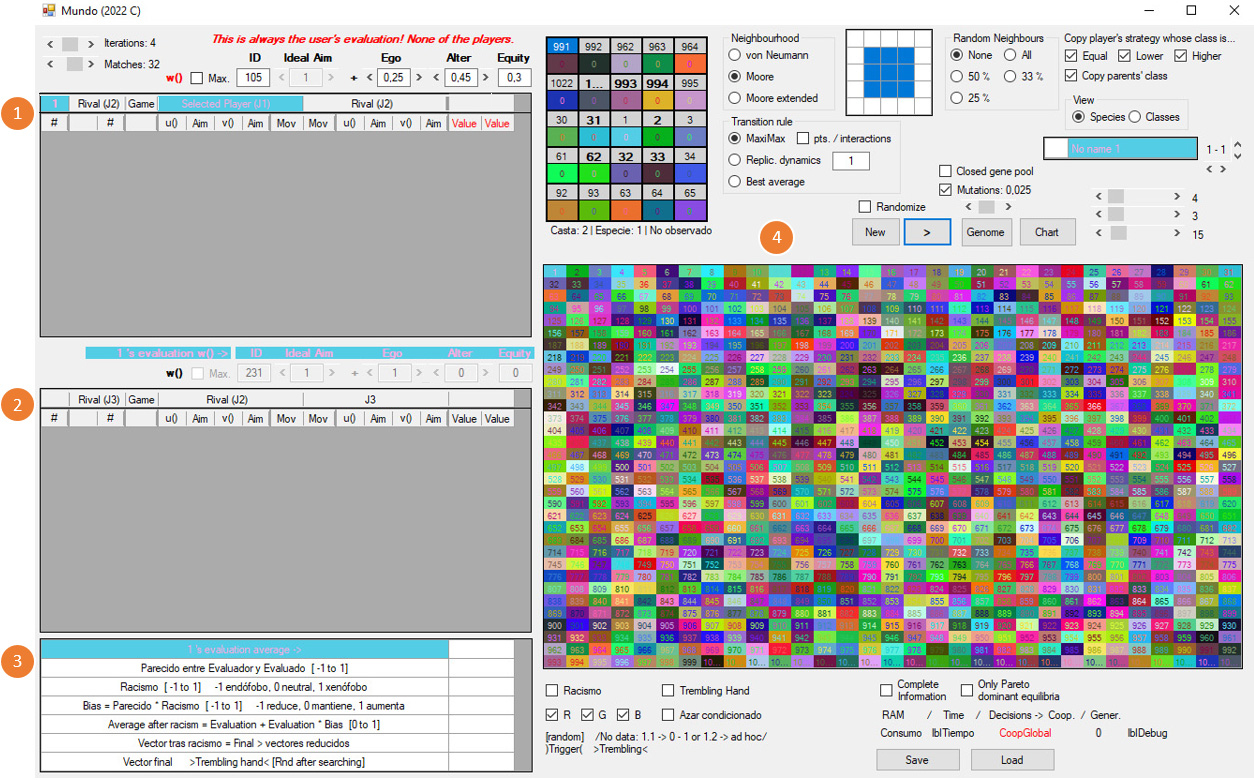
            Una vez puesta en marcha la simulación, y tras seleccionar un agente haciendo clic sobre él en el mapa, las tablas de historiales tienen un aspecto como éste:

 

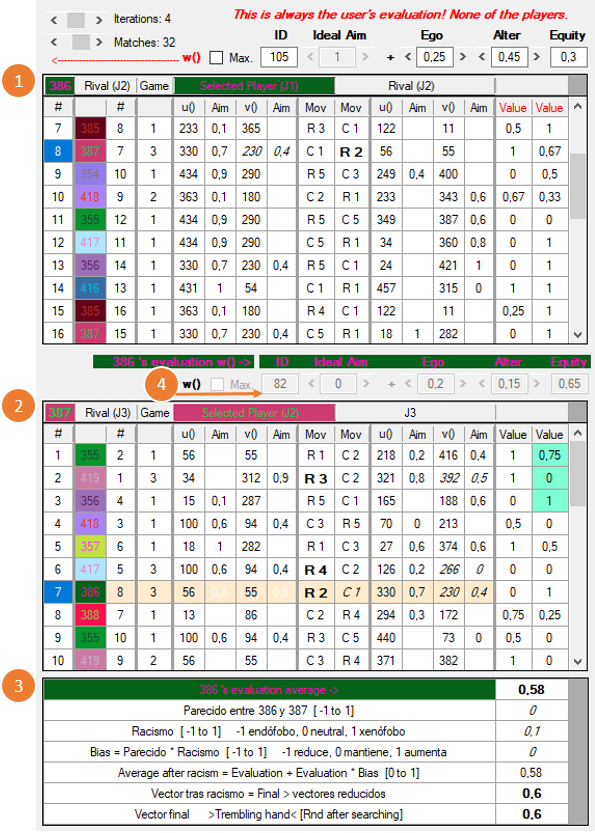
          Las tres tablas en la sección de historiales contienen la siguiente información:

1) Historial del jugador J1 (386 en el ejemplo), seleccionado en el mundo. Al hacer clic sobre algún jugador del mundo, en esta tabla se mostrarán todas sus interacciones en la generación que acaba de terminarr. En la columna 1 se indica en orden cronológico el número de cada interacción y en la columna 2 se enumeran todos los jugadores J2 con los que ha interactuado (355, 419, etc.) Desde las columnas 1 y 2 se puede obtener más información:
         1.1) Con un clic en la columna 1 de alguno de los J2 (el 387 en el ejemplo de arriba), en la tabla [2] aparecerán las interacciones de J2 contra una serie de jugadores, J3, enumerados en la columna 2 de la segunda tabla (355, 419, etc.). Además, en las matrices Matrix 0, 1, 2 y 3 de la ventana de inicio se verán los detalles de la interacción de J1 y J2. En Matrix 3 la función w será la que haya seleccionado el usuario.
         1.2) Con un clic en la columna 2, se invierten los papeles de J1 y J2: J2 pasará a mostrarse en la tabla [1] y J1, como uno de sus rivales, pasará a la tabla [2].
         La denominación “Rival” no es del todo afortunada, ya que sólo en los juegos de suma cero hay un antagonismo total, mientras que en muchos otros los intereses están parcialmente enfrentados y en algunos pueden incluso coincidir.

2) Historial de un jugador J2 (387 en el ejemplo), que ha interactuado con J1.
         2.1) Con un clic en la columna 1, en las matrices Matrix 0, 1, 2 y 3 de la ventana de inicio se verán los detalles de la interacción de J2 y J3. En Matrix 3 la función w será la que haya empleado J1 para evaluar los movimientos de J2 y J3.
         2.2) Con un clic en la columna 2, el J3 correspondiente pasará a mostrarse como J1 en la tabla [1].

3) Tabla de evaluación. Aquí se muestra la valoración final que J1 ha hecho de las decisiones o movimientos de J2. En orden descendente, las filas de esta tabla muestran los siguientes datos:

3.1) Valoración media e de los movimientos de J2, según la w de J1, que en este caso es 82 [4].

Hasta ahora, la valoración de las conductas observadas ha sido el único criterio considerado para de tomar una decisión. Sin embargo, esta simulación procura ser también un modelo de otros factores que pueden intervenir en un proceso de deliberación. En particular, se pueden incorporar algo así como “la clase social” a la que pertenece un individuo, de lo cual me ocuparé más adelante, y el aspecto externo del otro agente. Las  filas 2 – 5 de esta tercera tabla son un desglose del modo en que la percepción y la disposición o “prejuicio” hacia el aspecto externo del otro agente puede provocar una distorsión en la evaluación total y la consiguiente acción que termine por elegir.

3.2) Semejanza en el aspecto externo o fenotipo (básicamente el color) de J1 y J2. Esto es un elemento objetivo. La mayor diferencia posible, que se daría entre un jugador absolutamente negro y otro absolutamente blanco, se representa como -1, y la mayor semejanza posible, cuando ambos colores son idénticos, se representa como 1.

3.3) Grado de sensibilidad de J1 a las diferencias de color, también expresable como grado de racismo. Esto sería un elemento subjetivo y viene dado en los genes del agente artificial. Ahora bien, el racismo no sólo se expresa como sensibilidad a la diferencia, sino también a la semejanza. Así, un grado 0 indicaría la total indiferencia al grado de parecido, 1 indicaría una valoración negativa de lo diferente o ajeno (xenofobia), y -1 denotaría el fenómeno del rechazo a lo propio o semejante (endofobia).

3.4) De multiplicar el grado de semejanza (3.2) por el grado de racismo (3.3) resulta un índice de distorsión (bias) que modifica la media obtenida en 3.1. En sus valores extremos, -1 y 1, la distorsión puede reducir al mínimo o aumentar al máximo e, mientras que una distorsión de 0 deja invariable dicha media (3.1); todos los demás valores en el continuo entre -1 y 1 la modificarán proporcionalmente. Conviene notar que términos como xenofobia o endofobia son una mera etiqueta que indica la dirección en la que se desplaza la elección de una función en U, pero bien puede ocurrir, por ejemplo, que a resultas de una modificación producida por un alto grado de xenofobia la función u escogida sea muy cooperativa. Las distorsiones que modifican e entre 0 y 1 sólo indican un desplazamiento, pero qué respuesta corresponda al desplazamiento puede ser cualquier cosa.

3.5) Media definitiva, obtenida tras aplicar la distorsión del racismo (3.4) al valor e obtenido en 3.1. Observaciones:

3.5.1) Para que las operaciones descritas de 3.2 a 3.5 tengan efecto, la casilla “Racismo”, debajo del mapa del mundo, debe estar seleccionada. Si no lo está, los valores de las filas 2, 3 y 4 de la tabla de evaluación aparecerán en cursiva, y el valor de la fila 5 debería ser siempre el mismo de la fila 1.

3.5.2) Cuando la casilla “Racismo” está activada, debajo de ella pueden seleccionarse qué componentes del color (rojo, verde y azul) serán tenidos en cuenta al calcular la semejanza.

3.5.3) La sensibilidad al color puede emplearse como modelo de otros tipos de influencia. La he empleado, por ejemplo, para representar el envío y recepción de señales en el juego de la caza del venado con intercambio de información que analiza Skyrms en The Stag Hunt and the Evolution of Social Strucutre (pp. 67 - 81).

3.6) El resultado final es un número entre 0 y 1, en intervalos de 0.1, que apunta a la función u que será seleccionada de U y la función v, de V. Además de la distorsión que produce el racismo, este resultado final puede modificarse por el fenómeno conocido como “trembling hand” o por una elección al azar vinculada a cierto valor de u. Me ocuparé de estas dos posibilidades más adelante.

            Volvemos ahora a las tablas de historiales, para explicar el significado de los valores que aparecen en sus columnas.

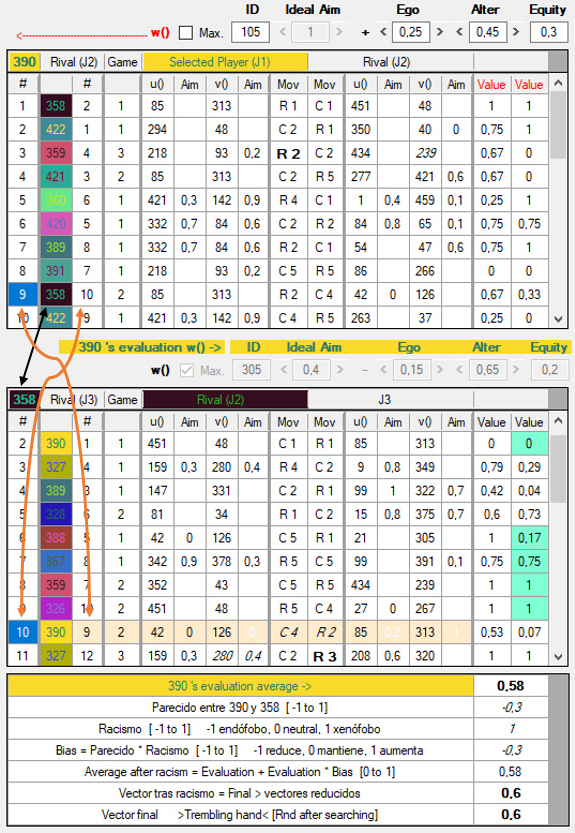
figura X

            En la tabla superior vemos el historial del jugador 390, al que consideraremos J1. En cada fila de la lista se ofrecen detalles de la interacción de J1 con una serie de rivales, a cada uno de los cuales denominaremos J2.  Las columnas, de izquierda a derecha, contienen la siguiente información:

            1) #: Número de interacción n_x de J1 (390). Esta columna simplemente muestra números sucesivos que ordenan los encuentros de J1 con  otros jugadores, desde el primero al último, en la generación que acaba de concluir.

            2) Rival: El número de J2, con quien ha interactuado J1. Así, por ejemplo, en su primera jugada J1 ha interactuado con J2 = 358, en la segunda contra J2 = 422, etc.

            3) Rival #: El número de interacción m_x de J2. Vemos que en su interacción n₉, J1 ha jugado con J2 = 358, y ésta ha sido la interacción m₁₀  de J2. Si hacemos clic en el “9” de la columna 1, se mostrará en la segunda tabla el historial de J2 = 358 y, en efecto, vemos allí que su décima interacción (columna 1) ha sido con J1 = 390 (columna 2) y que esa ha sido la novena interacción de J1 (columna 3). En definitiva, en la tabla 2 se muestra el historial del J2 seleccionado en la primera columna de la tabla 1.

            4) Game: Juego en el que han interactuado. El número corresponde al lugar que ocupa en la lista de juegos de la ventana principal (el juego 1, por ejemplo, es el dilema del prisionero).

            5) u(): Función de utilidad u1 que ha empleado J1 para valorar los pagos materiales del juego.

          6) Aim: Si está en blanco, significa que u1 es una función maximizadora. Si en ella aparece un número, indica que u1 es una función deontológica, y dicho número indica el grado de cumplimiento que la función busca alcanzar.

         7) v(): Función de utilidad v1 que, en la estimación de J1, J2 ha empleado para valorar los pagos materiales del juego. En juegos de información completa o en juegos sucesivos donde J2 ha movido primero, este valor aparece en cursiva, para indicar que la función v1 conjeturada no se tiene en cuenta y, en su lugar, J1 sabe qué función u2 ha empleado realmente J2 para valorar los pagos materiales. En la siguiente imagen se ven los detalles de un juego simultáneo de información completa: en la ventana de la derecha (ventana del mundo) el jugador seleccionado, J1, ha elegido columnas, de manera que en la ventana principal (a la izquierda) se presenta como jC. En cualquier caso, espero que se entienda: u1 (u_c en la ventana principal) = 154 es conocida directamente como v2 (v_f en la ventana principal); y lo mismo, pero a la inversa, para la función 86 de J2 (jF en la ventana principal). Las funciones v1 = 177 y v2 = 388 no se tienen en cuenta.

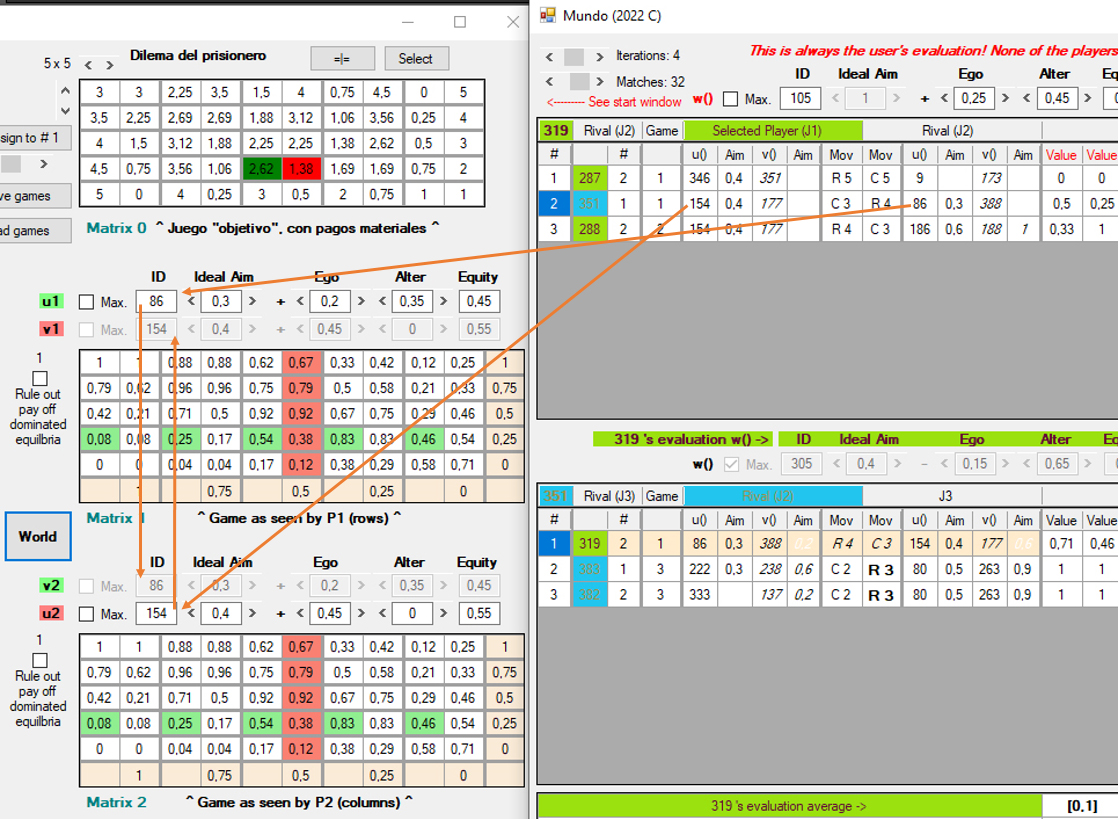
          8) Aim: véase (6), aplicable aquí a v1.

          9) Mov: Es el movimiento, expresado como R (row = fila) o C (columna) que ha seleccionado J1 en el juego (por ejemplo, R2). Si aparece marcada en negrita, significa que se trataba de un juego sucesivo y J1 ha movido primero. Por ejemplo, si volvemos a la tabla 1 de la figura X, en la tercera fila vemos que la columna Game contiene el juego del ultimátum (3), cuyos movimientos son sucesivos, y J1 (390) ha movido primero eligiendo la fila 3 (R2).

          10) Mov: Semejante a (7), muestra el movimiento (fila o columna) que ha seleccionado J2. Del mismo modo, si aparece marcada en negrita, significa que se trataba de un juego sucesivo y J2 ha movido primero.

         11) u(): Semejante a (5), es la función de utilidad u2 que ha empleado J2 para valorar los pagos materiales del juego.

          12) Aim: véase (6), aplicable a u2.

         13) v(): Semejante a (7), es la función de utilidad v2 que J2 le atribuye a J1.

          14) Aim: véase (8), aplicable a v2.

         15) Valoración del usuario del movimiento de J1 (tabla 1) o de J1 del movimiento de J2 (tabla 2)

         16) Valoración del usuario del movimiento de J2 (tabla 1) o de J1 del movimiento de J3 (tabla 2)

         Al seleccionar en la tabla 1 la jugada 9 de J1, vemos en la tabla 2 cómo J1 evaluó una serie de interacciones de J2. En este caso particular, el primer criterio de búsqueda de J1 es del tipo 2 y el segundo criterio, de tipo 3:

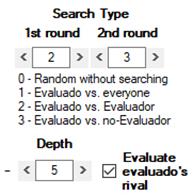
          La profundidad (depth) de la búsqueda es de 5 movimientos, comenzando por el más reciente y yendo hacia atrás (signo negativo -). Así, J1 busca 5 interacciones de J2 (evaluado) con el propio J1 (evaluador). Si el juego fuese sucesivo y J2 moviese primero, la primera de las interacciones examinadas podría ser la que está teniendo lugar en ese momento, marcada en color beige a lo largo de toda la fila. Sin embargo, como aquí se trata de un juego simultáneo, no hay nada que J1 pueda ver en la jugada presente, y retrocede por el historial de J2, hasta llegar a la jugada #2 de éste, marcada en azul claro en la columna 16. Con esto ha examinado una interacción, pero como el segundo criterio de búsqueda es del tipo 3, busca 4 jugadas más en las interacciones de J2 contra cualquier otro jugador, con lo cual observa las jugadas 9, 8, 7 y 6 de J2, todas ellas marcadas también en azul claro en la columna 16. Se señalan en esta columna porque el genoma de J1 tiene marcada la casilla Evaluate evaluado’s rival, lo que determina que J1 evalúe los movimientos de los diversos J3 (evaluado’s rival) contra J2 (evaluado), y no propiamente los movimientos de J2, que se muestran en la columna 15. Puesto que J2 (358) juega en su interacción #2 con J3 (390), y como 390 es el propio J1, éste está evaluando su propio movimiento.

            Seguimos en la figura X. De todos los valores marcados en azul claro se obtiene la media, 0.58, indicada en la primera fila de la tabla 3. A esta media se le aplican eventualmente distorsiones y modificaciones, tal como se explicó más arriba. El resultado final, redondeado a un decimal, se muestra en la última fila de la tabla 3. Si fuésmos a la ventana Genoma, observaríamos que los valores de U y V en 0.6 son 85 y 313, respectivamente, ambos con la la casilla Max./Grado en blanco, indicador de que son funciones maximizadoras. Estos valores de u y v deberán coincidir con los mostrados en las columnas 5 – 8 de la tabla 1 (de no ser así, algo está funcionando mal en el programa y agradecería mucho que me lo hiciesen saber).

 

Caso práctico: equilibrio evolutivamente estable (EEE)
con estrategias mixtas en el juego del gallina

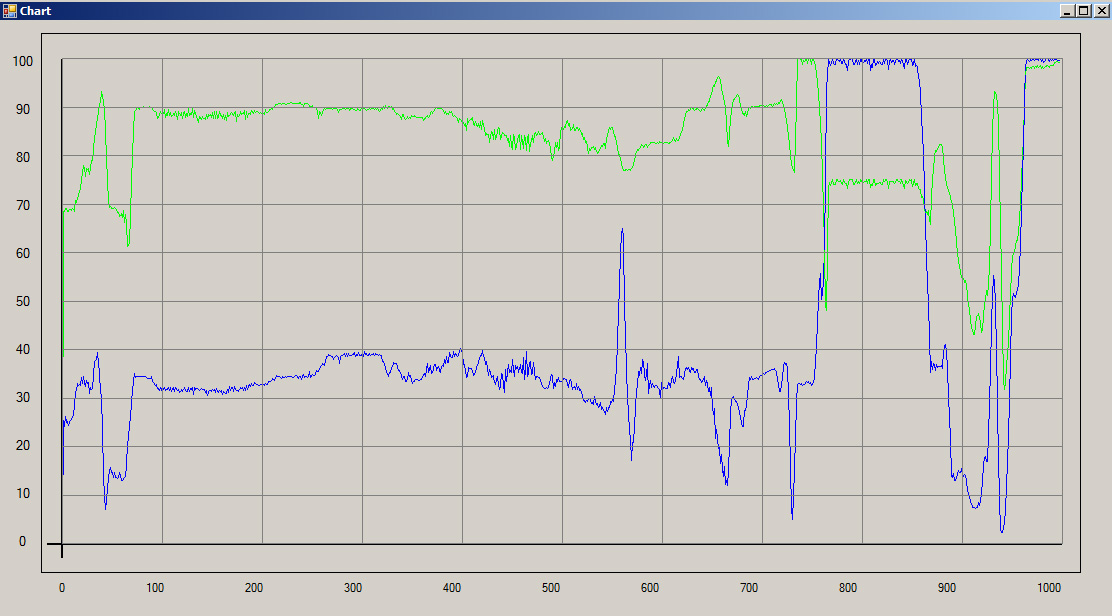
             En Evolution and the Theory of Games (cap. 2) Maynard Smith estudia el modelo de una población en la que todos los individuos juegan al juego del gallina a lo largo de varias generaciones. Hay dos tipos de jugadores: los cooperadores incondicionales (CI), que cooperan siempre, y los defectores incondicionales (DI), que defraudan invariablemente. Según la teoría, para dos agentes racionales la solución del juego del gallina consiste en emplear sendas estrategias mixtas, con cierta probabilidad p de cooperar y 1 – p de defraudar. Sin embargo, los agentes del modelo de Maynard Smith no pueden elegir al azar las estretegias puras que conforman la estrategia mixta, sino que cooperan o defraudan siempre. Lo notable es que una población inicial compuesta por cualquier proporción de CIs y DIs converge hacia una población en la que el p % de los individuos son CIs y el 100 – p % son DIs. Así, resulta que un proceso ciego de selección natural “elige” la estrategia mixta que escogería un agente perfectamente racional.

         Para realizar este experimento, con el botón Load games cargamos desde la ventana principal la configuración de juegos del archivo chicken_probabilidades.gms. Una vez cargado, si hacemos clic en el sexto juego de la lista, veremos esto: 

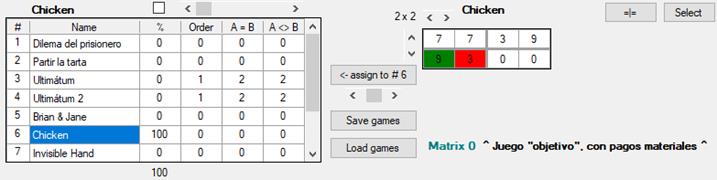
[Figura]

En la tercera columna, donde se muestra la frecuencia con la que se presentarán los diferentes juegos en el mundo, vemos que el único juego será siempre el del gallina (100 %).

      Luego hacemos clic en el botón World para abrir la ventana que contiene el mapa del mundo. En ella, abajo a la derecha, se encuentra el botón Load. Hacemos clic en él y cargamos la configuración del mundo del archivo chicken_probabilidades.wld, que contiene las siguientes propiedades del entorno.

1) Iterations: 1 y Matches: 1. En cada generación, los encuentros entre un mismo par de jugadores sólo se producen una vez; no hay repetición de interacciones. Además, cada jugador se encuentra (match) una única vez con algún jugador del mundo. Por ejemplo, si un agente está en un vecindario de 8 jugadores, de todos modos sólo interactuará con uno de ellos.

2) Tipo de vecindario Moore extended: cada jugador está en un vecindario de 24 jugadores. Aunque sólo va a jugar con uno de ellos (Matches: 1), este vecindario permite que el “radio” de posibles encuentros sea mayor, por ejemplo, que en un vecindario de 8 jugadores. En el modelo de Maynard Smith, el vecindario es la población en su totalidad. Por otra parte, aunque cada jugador sólo interactúa con uno de sus vecinos, puede copiar o heredar la estrategia de cualquiera de los 24.

3) Vecinos al azar: todos (All). De los 24 vecinos que rodean a un jugador dado, ninguno de ellos está situado físicamente en sus inmediaciones, sino que puede estar en cualquier lugar del mapa. Además, los 24 vecinos aleatorios varían de generación en generación; con esto se consigue una aproximación mayor al supuesto mencionado anterioremente, a saber, que el vecindario de cada jugador sea toda la población.

4) Regla de transición: replicator dynamics. En el tránsito de una generación a otra, la cantidad de individuos que emplean una estrategia A será proporcional al rendmiento global de la estrategia A, U(A), en relación al rendimiento promedio de todas las estrategias, U (The Evolution of Social Contract, p. 52).

            Aquí conviene destacar la diferencia entre simulaciones que calculan directamente este resultado y lo trasladan a priori a un determinado reparto de estrategias en la población, por un lado, y las simulaciones empíricas (como la presente), por otro. En éstas, las interacciones son reales y, como resultado de ellas, los agentes van sumando puntos; el cálculo de U(A) sólo se realiza localmente, en un vecindario limitado, y empleando una lotería discreta, es decir, sin distribuir uniformemente las estrategias según proporciones calculadas a priori. Una prueba de la validez del modelo empírico es que, posteriormente, al hacer en el mundo un recuento de los individuos que emplean determinadas estrategias, la distribución apenas se desvía de lo previsto por el cálculo del modelo a priori.

5) No hay mutaciones: aunque la frecuencia de mutaciones es de 25 cada 1000 individuos por generación, la correspondiente casilla no está marcada.
Nota: aunque la opción Closed gene pool no tiene relevancia para este experimento, aún se encuentra implementada en el programa, por lo que conviene no emplearla. En el futuro, servirá para que las mutaciones no sean completamente aleatorias, sino que se produzcan dentro de unos límites establecidos en la ventana de edición del genoma.

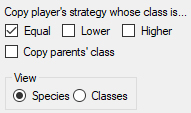
6) Las opciones Copy player’s strategy... filtran qué tipo de vecinos puede llegar a copiar un jugador. Las explicaré más adelante, en el contexto del trust game; en el presente experimento cada agente puede copiar a cualquiera de sus vecinos, de manera que deben estar todas seleccionadas.

7) Estas tres barras horizontales no tienen rótulos, aunque puede verse información sobre ellas al pasar el ratón por encima.

7.1 Mínimo para subsistir: dado un total de puntos p, si cada n interacciones el promedio por jugada, p / n, es inferior a la cantidad indicada aquí, el individuo “muere” y nadie puede volver a interactuar con él durante la generación en curso.

7.2 Número de interacciones n al cabo de las cuales se comprueba si el jugador ha obtenido al menos p / n puntos por interacción. Por ejemplo, si n es 3, la comprobación se hará al cabo de las jugadas 3, 6, 9, etc.

7.3 Mínimo para reproducirse: al cabo de una generación, un individuo tiene que haber reunido q puntos en total (no en promedio cada n jugadas) para poder reproducirse. Puede ocurrir que, aunque no llegue a completar el máximo de interacciones posibles de un generación porque en algún momento no ha cumplido la condición 7.1, haya reunido sin embargo suficientes puntos para reproducirse; podría verse como alguien que muere joven pero consigue reproducirse antes.

Las condiciones 7.3 no son relevantes para este experimento, y por eso sus valores son 0, 1 y 0; de todos modos las explico aquí ya que son parte de la configuración del mundo que puede guardarse y cargarse.

            Por último, vamos a cargar una serie de estrategias, guardadas en el archivo 2024_Chicken_probabilidades.txt. Para ello, desde la ventana del mundo hacemos clic en el botón Genome; se abrirá el editor de estrategias y, desde allí, hacemos clic en el botón Load, situado sobre la lista de la derecha:

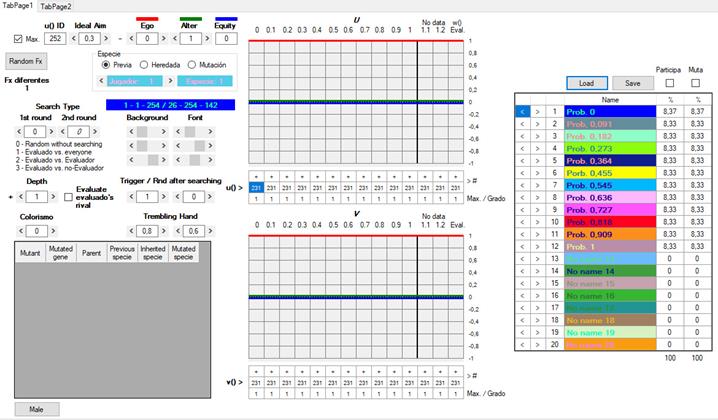
            En la columna que lleva el rótulo Participa se indica la participación inicial que tendrá cada estrategia en el mundo al iniciarse el experimento (la columna Muta está relacionada con la opción Closed gene pool y, como ya se ha mencionado, no tiene ninguna función en esta versión). En el caso que nos ocupa, las estrategias 1 – 12 tienen una distribución inicial aproximadamente equitativa, con una ligera ventaja para la estrategia 1:

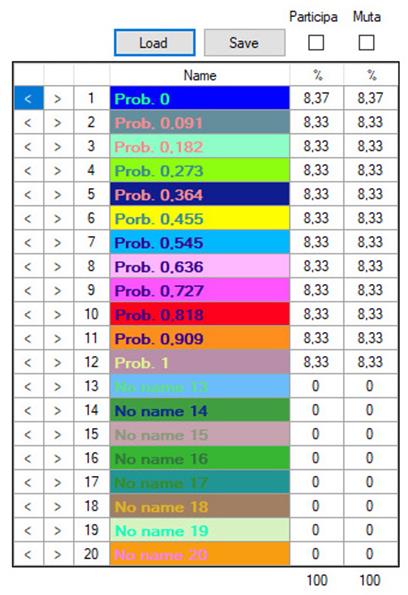
[Figura]

Para editar estos valores manualmente, basta con modificar el valor en cada casilla y confirmar con la tecla Tab. También se pueden seleccionar varias celdas y marcar o desmarcar la casilla Participa para distribuir uniformemente los porcentajes de participación entre las estrategias seleccionadas. Para nuestro experimento, arrastramos el ratón en la columna Participa, desde la fila 2 hasta la 11, de manera que esas estrategias quedarán seleccionadas. A continuación, marcamos la casilla Participa (no se producirá ningún cambio) y, por último, volvemos a desmarcar dicha casilla. Con esto habremos conseguido que sólo participen las estrategias 1 y 12, con una distribución inicial del 50 % cada una:

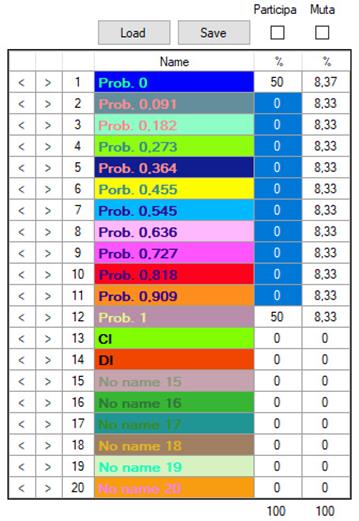
[Figura]

(Este procedimiento para seleccionar y distribuir estrategias se aplica también a la lista de juegos de la ventana inicial).

            La estrategia 1, designada como “Prob. 0” coopera con probabilidad 0, es decir, defrauda siempre, mientras que la estrategia “Prob. 1” coopera siempre (con probabilidad 1).

            Cerramos la ventana de edición de estrategias y en la ventana del mundo hacemos clic en New con el botón derecho del ratón para generar un nuevo mapa del mundo con una distribuición aleatoria de las estrategias que habíamos seleccionado en la ventana de edición de estrategias:

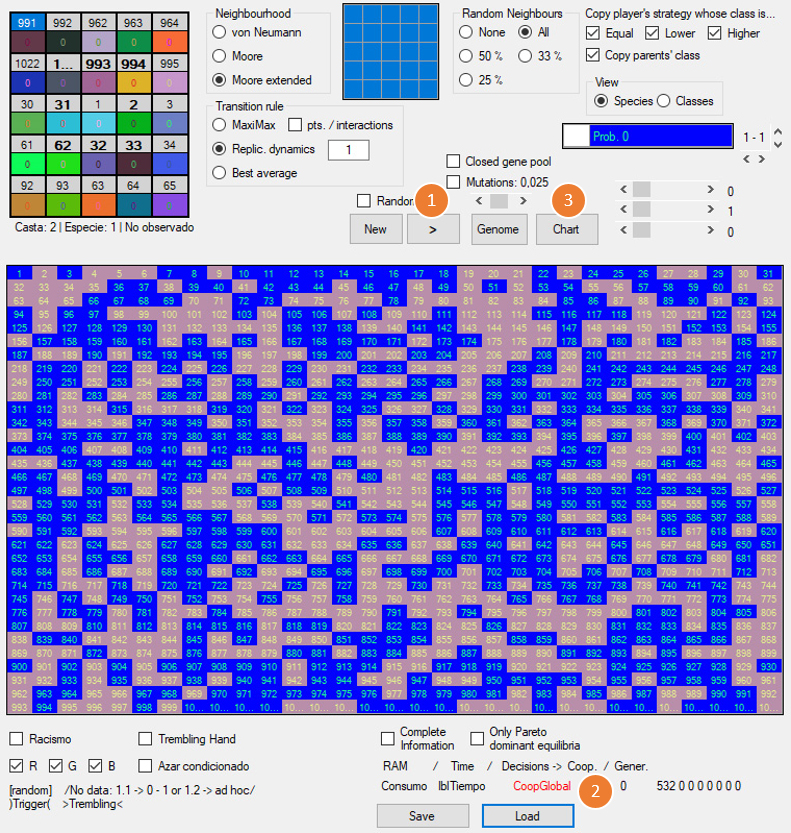
[Figura]

(Si hacemos clic en New con el botón principal, se inicia un mundo con una distribución inicial de estrategias generadas totalmente al azar).

            Para poner en marcha la simulación, hacemos clic en el botón "play" > [1], situado a la derecha New. Para detenerla, hacemos clic en el mismo botón, que ahora tendrá el símbolo || (pausa).

            A medida que se suceden las generaciones, podemos ir viendo que el grado de cooperación global (CoopGlobal [2]) fluctúa en torno a 0.6; es decir, que el 60 % de todas decisiones que han tomado los individuos en el mundo son cooperativas. Como los únicos agentes posibles son los que cooperan siempre o los que defraudan siempre, esto significa que la población está compuesta en un 60 % por cooperadores incondicionales, aunque al iniciarse la simulación eran sólo el 50 % de la población.

            Podemos volver a la ventana de edición de estrategias y asignar un 90 % a la estrategia 1 y un 10 % a la estrategia 12. Si reiniciamos el mundo y lo ponemos de nuevo en marcha, veremos que la población tiende rápidamente al polimorfismo 60 %  – 40 %.

            Tal como predice la teoría, éstas son las probabilidades con las que un agente perfectamente racional conformaría su estrategia mixta para maximizar la utilidad esperada en el juego del gallina con los pagos que de hecho tenemos en esta simulación:

	C 1	C 2
F 1	7 ; 7	3 ; 9
F 2	9 ; 3	0 ; 0

 

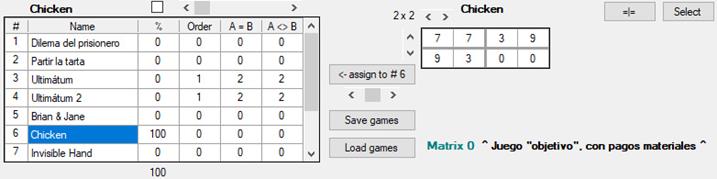
Es importante notar que este grado de cooperación global siempre está medido con una función de utilidad w definida por el usuario; en este caso, la función deontológica 105, que valora con 1 tanto la fila 1 como la columna 1, y valora con 0 la fila 2 y la columna 2.

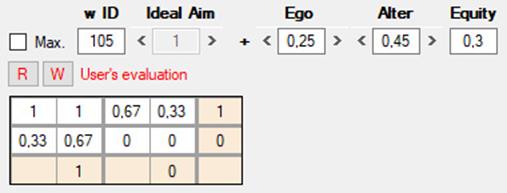
Para ver la evolución de la cooperación a lo largo del tiempo, desde la ventana del mundo podemos abrir la ventana de estadísticas haciendo clic en el botón Chart [3]:

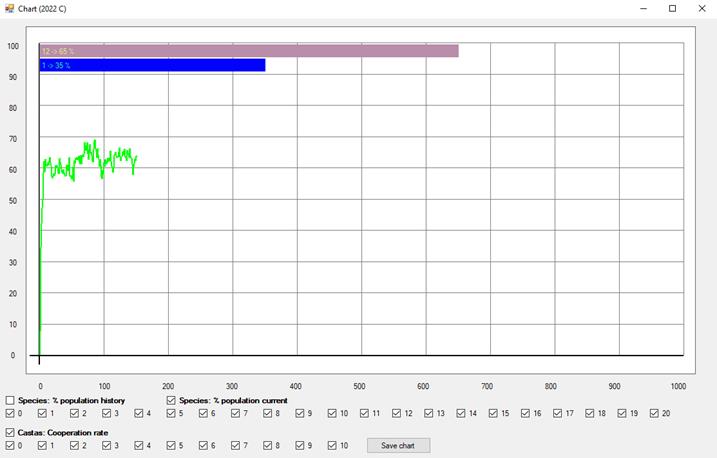
Para ver mejor el grado de cooperación general, representado por la línea verde, conviene desmarcar la casilla Species: % population history.

Este experimento admite diversas variaciones que vale la pena probar:
1) Cambiar los pagos: siempre que conserven la estructura del juego del gallina, el grado de cooperación global coincidirá con la probabilidad de cooperar en una estrategia mixta empleada por un agente perfectamente racional.
2) Incorporar otras estrategias entre las seleccionables en la lista del editor de estrategias, y no sólo estos dos casos extremos, que cooperan con probabilidad 1 o 0.
Designaremos como p₁ a la estrategia que coopera con probabilidad 1, p_0.9 a la que coopera con probabilidad 0.9, etc., hasta p₀, que es la estrategia que nunca coopera, mientras que p₁, p_0.9, … , p₀, serán las cantidades porcentuales de individuos presentes en la población que usan cada una de las 11 estrategias. Es interesante notar (esto no lo he visto en la literatura) que si incluimos más estrategias en el mundo, independientemente de la distribución inicial, siempre se cumple que

p₁ · q₁ + … + p₀ · q₀

es aproximadamente igual al grado de cooperación media de toda la población (en nuestro ejemplo 0.6), lo que a su vez equivale, como ya se indicó, a la probabilidad p con la que un agente racional elige una de las estrategias puras que componen la estrategia mixta que maximiza la utilidad esperada del juego.

El juego de la confianza (trust game)